
【题目】已知函数![]() 是奇函数,其中a>1.
是奇函数,其中a>1.
(1)求实数m的值;
(2)讨论函数f(x)的增减性;
(3)当![]() 时,f(x)的值域是(1,+∞),求n与a的值.
时,f(x)的值域是(1,+∞),求n与a的值.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,以2为半径的半圆弧![]() 所在平面垂直于矩形
所在平面垂直于矩形![]() 所在平面,
所在平面,![]() 是圆弧
是圆弧![]() 上异于
上异于![]() 、
、![]() 的点.
的点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)当四棱锥![]() 的体积最大为8时,求平面
的体积最大为8时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海产品经销商调查发现,该海产品每售出![]() 吨可获利
吨可获利![]() 万元,每积压
万元,每积压![]() 吨则亏损
吨则亏损![]() 万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
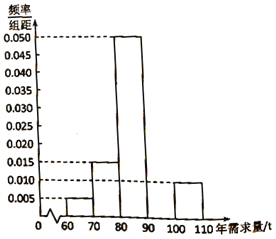
(1)请补齐![]() 上的频率分布直方图,并依据该图估计年需求量的平均数;
上的频率分布直方图,并依据该图估计年需求量的平均数;
(2)今年该经销商欲进货![]() 吨,以
吨,以![]() (单位:吨,
(单位:吨, ![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将![]() 表示为
表示为![]() 的函数解析式;并求今年的年利润不少于
的函数解析式;并求今年的年利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①命题“任意![]() ”的否定是“任意
”的否定是“任意![]() ;
;
②命题“若![]() ,则
,则![]() ”的逆否命题是真命题;
”的逆否命题是真命题;
③若命题![]() 为真,命题
为真,命题![]() 为真,则命题
为真,则命题![]() 且
且![]() 为真;
为真;
④命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”.
”.
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有50名学生,在一次考试中统计出平均分数为70,方差为75,后来发现有2名学生的成绩统计有误,学生甲实际得分是80分却误记为60分,学生乙实际得分是70分却误记为90分,更正后的平均分数和方差分别是( )
A. 70和50 B. 70和67 C. 75和50 D. 75和67
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com