
科目: 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为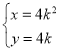 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() ,且直线
,且直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率![]() 与日产量
与日产量![]() (万件)之间满足关系:
(万件)之间满足关系: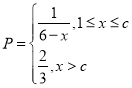 (
(![]() )已知每生产1万件合格的仪器可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.(注:次品率=次品数/生产量)
)已知每生产1万件合格的仪器可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.(注:次品率=次品数/生产量)
(1)试将生产这种仪器元件每天的盈利额![]() (万元)表示为日产量
(万元)表示为日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]()
(1)求![]() 的值;
的值;
(2)![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)函数的性质通常指的是函数的定义域、值域、单调性、周期性、奇偶性等,请你探究函数![]() 其中的三个性质(直接写出结论即可)
其中的三个性质(直接写出结论即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() :
:![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于两点
于两点![]() ,
,![]() ,当
,当![]() 恰好位于
恰好位于![]() 轴上时,
轴上时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市旅游局为了进一步开发旅游资源,需要了解游客的情况,以便制定相应的策略,在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下:若景点甲中的数据的中位数是126,景点乙中的数据的平均数是124.
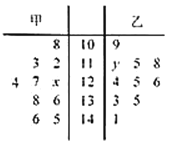
(1)求![]() ,
,![]() 的值;
的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据(视样本频率为概率).今从这段时期内任取4天,记其中游客数不低于125人的天数为![]() ,求概率
,求概率![]() ;
;
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于135人的天数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
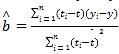 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com