练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥 中， 平面 ，底面是等腰梯形，且 ，其中 .

    （1）证明：平面 平面 .

    （2）求点 到平面 的距离。

    【答案】（1）见解析；（2）

    【解析】

    （1）由题意结合已知数据，利用勾股数证得，又由 平面可得，从而证得 平面，再利用面面垂直的判定定理可得结论.

    （2）先求得,利用余弦定理及三角形面积公式求得，利用等体积转化根据可得距离.

    （1）过点作交于点.

    因为底面 是等腰梯形，且 ，所以

    在 中， ，同理可得

    因为 与 相似，所以 ，

    所以 ，则

    因为 平面平面，所以

    因为 平面平面，且 ，所以 平面

    因为 平面 ，所以平面 平面

    （2）因为平面，所以 ，

    因为 ，所以

    在 中，因为 ，

    所以，

    所以 ，则的面积为

    设点到平面 的距离为，则三棱锥的体积

    因为 ，所以，解得

    故点到平面的距离为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知命题α：函数的定义域是R；命题β：在R上定义运算：xy=x（1-y）．不等式（x-a）（x+a）＜1对任意实数x都成立．

    （1）若α、β中有且只有一个真命题，求实数a的取值范围；

    （2）若α、β中至少有一个真命题，求实数a的取值范围；

    （3）若α、β中至多有一个真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB＝2a，F为CD的中点．

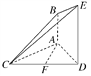
    (1)求证：AF∥平面BCE；

    (2)判断平面BCE与平面CDE的位置关系，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)若f (x)在区间(－∞，2)上为单调递增函数，求实数a的取值范围；

    (2)若a＝0，x0<1，设直线y＝g(x)为函数f (x)的图象在x＝x0处的切线，求证:f (x)≤g(x).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，，函数.

    （Ⅰ）设不等式的解集为C，当时，求实数取值范围；

    （Ⅱ）若对任意，都有成立，试求时，的值域；

    （Ⅲ）设，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备，通过市场分析，全年需投入固定成本3000万元，每生产x（百辆），需另投入成本万元，且，由市场调研知，每辆车售价6万元，且全年内生产的车辆当年能全部销售完.

    （1）求出2019年的利润（万元）关于年产量x（百辆）的函数关系式；（利润=销售额成本）

    （2）2019年产量为多少（百辆）时，企业所获利润最大？并求出最大利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：，其离心率为，以原点为圆心，椭圆的短轴长为直径的圆被直线截得的弦长等于.

    （1）求椭圆的方程；

    （2）设为椭圆的左顶点，过点的直线与椭圆的另一个交点为，与轴相交于点，过原点与平行的直线与椭圆相交于两点，问是否存在常数，使恒成立？若存在，求出；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设， 满足约束条件，则的最大值为_______．

    【答案】4

    【解析】,画出可行域如下图所示,由图可知,目标函数在点处取得最大值为.

    [点睛]本小题主要考查线性规划的基本问题,考查了指数的运算. 画二元一次不等式或表示的平面区域的基本步骤：①画出直线（有等号画实线，无等号画虚线）；②当时，取原点作为特殊点，判断原点所在的平面区域；当时，另取一特殊点判断；③确定要画不等式所表示的平面区域.

    【题型】填空题
    【结束】
    14

    【题目】已知数列的前项和公式为，若，则数列的前项和__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，圆的普通方程为. 在以坐标原点为极点，轴正半轴为极轴的极坐标系中，直线的极坐标方程为 .

    （Ⅰ） 写出圆 的参数方程和直线的直角坐标方程；

    （ Ⅱ ） 设直线 与轴和轴的交点分别为，为圆上的任意一点，求的取值范围.

    【答案】(1);.

    (2).

    【解析】【试题分析】(I)利用圆心和半径,写出圆的参数方程,将圆的极坐标方程展开后化简得直角坐标方程.(II)求得两点的坐标, 设点，代入向量,利用三角函数的值域来求得取值范围.

    【试题解析】

    （Ⅰ）圆的参数方程为（为参数）.

    直线的直角坐标方程为.

    （Ⅱ）由直线的方程可得点，点.

    设点，则 .

    .

    由（Ⅰ）知，则 .

    因为，所以.

    【题型】解答题
    【结束】
    23

    【题目】选修4-5：不等式选讲

    已知函数， .

    （Ⅰ）若对于任意， 都满足，求的值；

    （Ⅱ）若存在，使得成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案