【题目】已知函数.

(1)求曲线在点处的切线方程；

(2)证明：在区间上有且仅有个零点.

【题目】已知函数（e为自然对数的底数）．

（1）求函数的值域；

（2）若不等式对任意恒成立，求k的取值范围．

【题目】过抛物线）的焦点F且斜率为1的直线交抛物线C于M，N两点，且．

（1）求p的值；

（2）抛物线C上一点，直线（其中）与抛物线C交于A，B两个不同的点（A，B均与点Q不重合）．设直线QA，QB的斜率分别为.

（i）直线l是否过定点？如果是，请求出所有定点；如果不是，请说明理由；

（ii）设点T在直线l上，且满足，其中为坐标原点．当线段最长时，求直线l的方程．

【题目】如图，在三棱柱中，底面ABC为正三角形，底面ABC，，点在线段上，平面平面．

（1）请指出点的位置，并给出证明；

（2）若，求与平面ABE夹角的正弦值．

若规定问卷得分不低于70分的市民称为“动物保护关注者”，则山图中表格可得列联表如下：

（1）请判断能否在犯错误的概率不超过0．05的前提下认为“动物保护关注者”与性别有关？

（2）若问卷得分不低于80分的人称为“动物保护达人”．现在从本次调查的“动物保护达人”中利用分层抽样的方法随机抽取6名市民参与环保知识问答，再从这6名市民中抽取2人参与座谈会，求抽取的2名市民中，既有男“动物保护达人”又有女“动物保护达人”的概率．

附表及公式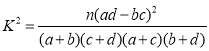：，其中.

【题目】如图，在直三棱柱中，已知，，，.是线段的中点.

（1）求直线与平面所成角的正弦值；

（2）求二面角的大小的余弦值.

【题目】已知函数，函数的图象在处的切线与直线平行.

（Ⅰ）求实数的值；

（Ⅱ）若函数存在单调递减区间，求实数的取值范围；

（Ⅲ）设()是函数的两个极值点，若，试求的最小值.

【题目】如图，在三棱锥中，平面平面，，，若为的中点.

（1）证明：平面；

（2）求异面直线和所成角；

（3）设线段上有一点，当与平面所成角的正弦值为时，求的长.

【题目】已知圆与椭圆相交于点M（0，1），N（0，-1），且椭圆的离心率为.

（1）求的值和椭圆C的方程；

（2）过点M的直线交圆O和椭圆C分别于A，B两点.

①若，求直线的方程；

②设直线NA的斜率为，直线NB的斜率为，问:是否为定值? 如果是，求出定值；如果不是，说明理由.

【题目】已知直线：与直线：的距离为，椭圆：的离心率为.

（1）求椭圆的标准方程；

（2）在（1）的条件下，抛物线：的焦点与点关于轴上某点对称，且抛物线与椭圆在第四象限交于点，过点作抛物线的切线，求该切线方程并求该直线与两坐标轴围成的三角形面积.