
科目: 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务的时间的统计数据如下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95多的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |

查看答案和解析>>
科目: 来源: 题型:
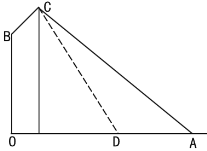
【题目】如图,在路边安装路灯:路宽![]() 米,灯杆长
米,灯杆长![]() 米,且与灯柱
米,且与灯柱![]() 成120°角,路灯采用锥形灯罩,灯罩轴线
成120°角,路灯采用锥形灯罩,灯罩轴线![]() 与灯杆垂直且正好通过道路路面的中线.
与灯杆垂直且正好通过道路路面的中线.
(1)求灯柱高![]() 的长度(精确到0.01米);
的长度(精确到0.01米);
(2)若该路灯投射出的光成一个圆锥体,该圆锥体母线与轴线的夹角是30°,写出路灯在路面上投射出的截面图形的边界是什么曲线?写出其相应的几何量(精确到0.01米).
查看答案和解析>>
科目: 来源: 题型:
【题目】给定椭圆![]() ,称圆心在坐标原点
,称圆心在坐标原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“伴椭圆”,若椭圆
的“伴椭圆”,若椭圆![]() 右焦点坐标为
右焦点坐标为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的“伴椭圆”方程;
的“伴椭圆”方程;
(2)在椭圆![]() 的“伴椭圆”上取一点
的“伴椭圆”上取一点![]() ,过该点作椭圆的两条切线
,过该点作椭圆的两条切线![]() 、
、![]() ,证明:两线垂直;
,证明:两线垂直;
(3)在双曲线![]() 上找一点
上找一点![]() 作椭圆
作椭圆![]() 的两条切线,分别交于切点
的两条切线,分别交于切点![]() 、
、![]() 使得
使得![]() ,求满足条件的所有点
,求满足条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】图(1)为东方体育中心,其设计方案侧面的外轮廓线如图(2)所示;曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() 且
且![]() 恰好等于圆
恰好等于圆![]() 的半径,
的半径,![]() 与圆相切且
与圆相切且![]() .
.
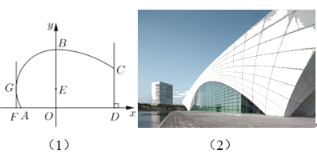
(1)若要求![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)当![]() 时,若要求
时,若要求![]() 不超过45米,求
不超过45米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】“90后”指1990年及以后出生,“80后”指1980-1989年之间出生,“80前”指1979年及以前出生.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( )

A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,对于一切
时,对于一切![]() ,函数
,函数![]() 在区间
在区间![]() 内总存在唯一零点,求
内总存在唯一零点,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,数列
时,数列![]() 的前
的前![]() 项和
项和![]() ,若
,若![]() 是单调递增数列,求
是单调递增数列,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,函数
时,函数![]() 在区间
在区间![]() 内的零点为
内的零点为![]() ,判断数列
,判断数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的增减性,并说明理由.
的增减性,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某景区欲建两条圆形观景步道![]() (宽度忽略不计),如图所示,已知
(宽度忽略不计),如图所示,已知![]() ,
,![]() (单位:米),要求圆M与
(单位:米),要求圆M与![]() 分别相切于点B,D,圆
分别相切于点B,D,圆![]() 与
与![]() 分别相切于点C,D.
分别相切于点C,D.
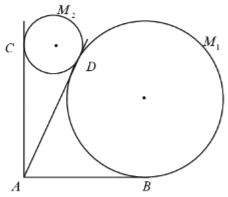
(1)若![]() ,求圆
,求圆![]() 的半径;(结果精确到0.1米)
的半径;(结果精确到0.1米)
(2)若观景步道![]() 的造价分别为每米0.8千元与每米0.9千元,则当
的造价分别为每米0.8千元与每米0.9千元,则当![]() 多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 经过
经过![]() 两点,且圆心
两点,且圆心![]() 在直线
在直线![]() 上.
上.

(1)求圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交截得的弦长为
相交截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)已知点![]() ,在平面内是否存在异于点
,在平面内是否存在异于点![]() 的定点
的定点![]() ,对于圆
,对于圆![]() 上的任意动点
上的任意动点![]() ,都有
,都有![]() 为定值?若存在求出定点
为定值?若存在求出定点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com