练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

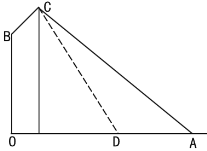
    【题目】如图，在路边安装路灯：路宽米，灯杆长米，且与灯柱成120°角，路灯采用锥形灯罩，灯罩轴线与灯杆垂直且正好通过道路路面的中线.

    （1）求灯柱高的长度（精确到0.01米）；

    （2）若该路灯投射出的光成一个圆锥体，该圆锥体母线与轴线的夹角是30°，写出路灯在路面上投射出的截面图形的边界是什么曲线？写出其相应的几何量（精确到0.01米）.

    【答案】（1）16.25米；（2）边界是椭圆，长轴长为31.61米，短轴长为21.07米，焦距长为23.56米.

    【解析】

    （1）先建立平面直角坐标系，再求出直线的点斜式方程即可；

    （2）路灯在路面上投射出的截面图形的边界是椭圆，再求出其长轴长、短轴长及焦距长即可.

    解：（1）建立以为坐标原点，所在直线为轴，所在直线为轴的直角坐标系，设，则，因为直线的倾斜角为120°，

    所以直线的方程为：，

    将代入得：，所以 米；

    （2）路灯在路面上投射出的截面图形的边界是椭圆，

    由已知可得该椭圆的长轴长为米，

    短轴长为米，

    焦距长为米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，12月1日至12月5日的昼夜温差与实验室每天每100颗种子中的发芽数如下表所示：

    日期

    12月1日

    12月2日

    12月3日

    12月4日

    12月5日

    温差x(℃)

    10

    11

    13

    12

    8

    发芽数y(颗)

    23

    25

    30

    26

    16

    该农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求回归方程，再用被选取的2组数据进行检验．

    (1)求选取的2组数据恰好是不相邻的2组数据的概率．

    (2)若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求y关于x的线性回归方程.

    (3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗，则认为得到的线性回归方程是可靠的，试问(2)中所得的线性回归方程是否可靠？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数是由曲线确定的．

    （1）写出函数，并判断该函数的奇偶性；

    （2）求函数的单调区间并证明其单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，．

    （1）若函数f（x）在处有极值，求函数f（x）的最大值；

    （2）是否存在实数b，使得关于x的不等式在上恒成立？若存在，求出b的取值范围；若不存在，说明理由；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）当时，对于一切，函数在区间内总存在唯一零点，求的取值范围；

    （2）当时，数列的前项和，若是单调递增数列，求的取值范围；

    （3）当，时，函数在区间内的零点为，判断数列、、、、的增减性，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆的离心率为，圆与正半轴交于点，圆在点处的切线被椭圆截得的弦长为.

    （1）求椭圆的方程；

    （2）设圆上任意一点处的切线交椭圆于点、，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的单调性；

    （2）若有两个零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某居民区随机抽取10个家庭，获得第个家庭的月收入（单位：千元）与月储蓄（单位：千元）的数据资料，算得，，，．

    （1）求家庭的月储蓄对月收入的线性回归方程；

    （2）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．

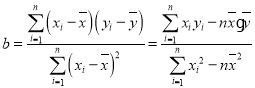    （附：线性回归方程中，，其中，为样本平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量．镇有基层干部60人,镇有基层干部60人,镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,,绘制成如图所示的频率分布直方图．

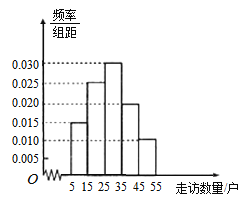
    (1)求这40人中有多少人来自镇,并估计三镇的基层干部平均每人走访多少贫困户；(同一组中的数据用该组区间的中点值作代表)

    (2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为,求的分布列及数学期望．

    查看答案和解析>>

    同步练习册答案