
【题目】设函数![]() 是由曲线
是由曲线![]() 确定的.
确定的.
(1)写出函数![]() ,并判断该函数的奇偶性;
,并判断该函数的奇偶性;
(2)求函数![]() 的单调区间并证明其单调性.
的单调区间并证明其单调性.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设命题p:实数![]() 满足不等式
满足不等式![]() ;
;
命题q:关于![]() 不等式
不等式![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 上有最大值
上有最大值![]() 和最小值
和最小值![]() ,设
,设![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了![]() 年下半年该市
年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工月工资的中位数为
名农民工月工资的中位数为![]() 百元(假设这
百元(假设这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内)且月工资收入在
(百元)内)且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:
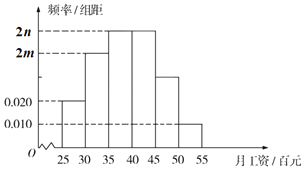
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名,则能否在犯错误的概率不超过
名,则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: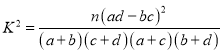 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
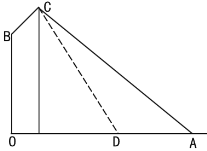
【题目】如图,在路边安装路灯:路宽![]() 米,灯杆长
米,灯杆长![]() 米,且与灯柱
米,且与灯柱![]() 成120°角,路灯采用锥形灯罩,灯罩轴线
成120°角,路灯采用锥形灯罩,灯罩轴线![]() 与灯杆垂直且正好通过道路路面的中线.
与灯杆垂直且正好通过道路路面的中线.
(1)求灯柱高![]() 的长度(精确到0.01米);
的长度(精确到0.01米);
(2)若该路灯投射出的光成一个圆锥体,该圆锥体母线与轴线的夹角是30°,写出路灯在路面上投射出的截面图形的边界是什么曲线?写出其相应的几何量(精确到0.01米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() ,
,![]() 为椭圆上任意一点,证明:点
为椭圆上任意一点,证明:点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 距离的
距离的![]() 倍.
倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com