
【题目】已知椭圆![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() ,
,![]() 为椭圆上任意一点,证明:点
为椭圆上任意一点,证明:点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 距离的
距离的![]() 倍.
倍.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
(附:线性回归方程![]() 中,
中,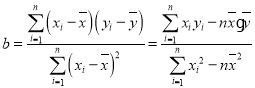 ,其中
,其中![]() ,
,![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大数据时代对于现代人的数据分析能力要求越来越高,数据拟合是一种把现有数据通过数学方法来代入某条数式的表示方式,比如![]() ,
,![]()
![]() ,2,
,2,![]() ,n是平面直角坐标系上的一系列点,用函数
,n是平面直角坐标系上的一系列点,用函数![]() 来拟合该组数据,尽可能使得函数图象与点列
来拟合该组数据,尽可能使得函数图象与点列![]() 比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数
比较接近.其中一种描述接近程度的指标是函数的拟合误差,拟合误差越小越好,定义函数![]() 的拟合误差为:
的拟合误差为:![]() .已知平面直角坐标系上5个点的坐标数据如表:
.已知平面直角坐标系上5个点的坐标数据如表:
x | 1 | 3 | 5 | 7 | 9 |
y | 12 |
| 4 |
| 12 |
![]() 若用一次函数
若用一次函数![]() 来拟合上述表格中的数据,求该函数的拟合误差
来拟合上述表格中的数据,求该函数的拟合误差![]() 的最小值,并求出此时的函数解析式
的最小值,并求出此时的函数解析式![]() ;
;
![]() 若用二次函数
若用二次函数![]() 来拟合题干表格中的数据,求
来拟合题干表格中的数据,求![]() ;
;
![]() 请比较第
请比较第![]() 问中的
问中的![]() 和第
和第![]() 问中的
问中的![]() ,用哪一个函数拟合题目中给出的数据更好?
,用哪一个函数拟合题目中给出的数据更好?![]() 请至少写出三条理由
请至少写出三条理由![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆
是椭圆![]() 上一点,当
上一点,当![]() 时,有
时,有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点,试问:在
两点,试问:在![]() 铀上是否存在与
铀上是否存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立?
恒成立?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全国第五个“扶贫日”到来之前,某省开展“精准扶贫,携手同行”的主题活动,某贫困县调查基层干部走访贫困户数量.![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部60人,
镇有基层干部60人,![]() 镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从
镇有基层干部80人,每人都走访了若干贫困户,按照分层抽样,从![]() 三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,
三镇共选40名基层干部,统计他们走访贫困户的数量,并将走访数量分成5组,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
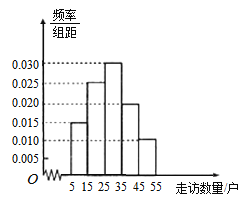
(1)求这40人中有多少人来自![]() 镇,并估计
镇,并估计![]() 三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
三镇的基层干部平均每人走访多少贫困户;(同一组中的数据用该组区间的中点值作代表)
(2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从![]() 三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为
三镇的所有基层干部中随机选取3人,记这3人中工作出色的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com