
科目: 来源: 题型:
【题目】甲、乙两位同学参加某个知识答题游戏节目,答题分两轮,第一轮为“选题答题环节”第二轮为“轮流坐庄答题环节”.首先进行第一轮“选题答题环节”,答题规则是:每位同学各自从备选的5道不同题中随机抽出3道题进行答题,答对一题加10分,答错一题(不答视为答错)减5分,已知甲能答对备选5道题中的每道题的概率都是![]() ,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第
,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第![]() 道题也由该同学(最先答题的同学)作答的概率为
道题也由该同学(最先答题的同学)作答的概率为![]() (
(![]() ),其中
),其中![]() ,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是
,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是![]() ,如果某位同学有机会答第
,如果某位同学有机会答第![]() 道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
(1)请预测第二轮最先开始作答的是谁?并说明理由
(2)①求第二轮答题中![]() ,
,![]() ;
;
②求证![]() 为等比数列,并求
为等比数列,并求![]() (
(![]() )的表达式.
)的表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.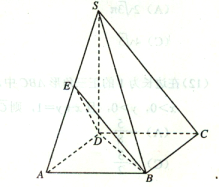
查看答案和解析>>
科目: 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”.三国时期,吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形中较小的锐角![]() ,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
,现在向该正方形区域内随机地投掷100枚飞镖,则估计飞镖落在区域1的枚数最有可能是( )
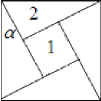
A.30B.40C.50D.60
查看答案和解析>>
科目: 来源: 题型:
【题目】诚信是立身之本,道德之基,我校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一周期 |
|
|
|
|
第二周期 |
|
|
|
|
第三周期 |
|
|
|
|
(Ⅰ)计算表中十二周“水站诚信度”的平均数![]() ;
;
(Ⅱ)若定义水站诚信度高于![]() 的为“高诚信度”,
的为“高诚信度”,![]() 以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率;
以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率;
(Ⅲ)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的准线方程为x=﹣1.
(1)求抛物线C的方程;
(2)过抛物线C的焦点作直线l,交抛物线C于A,B两点,若线段AB中点的横坐标为6,求|AB|.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() ,前n项和为
,前n项和为![]() ,对任意的正整数n,都有
,对任意的正整数n,都有![]() 恒成立.
恒成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知关于n的不等式![]() …
…![]() 对一切
对一切![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)已知 ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小并证明.
的大小并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com