【题目】首届世界低碳经济大会在南昌召开，本届大会以“节能减排，绿色生态”为主题，某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品．已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本(元)与月处理量(吨)之间的函数关系可近似地表示为，且每处理一吨二氧化碳得到可利用的化工产品价值为100元．

（1）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？

（2）该单位每月能否获利？如果获利，求出最大利润；如果不获利，则需要国家至少补贴多少元才能使该单位不亏损？

【题目】以坐标原点为极点，以轴的非负半轴为极轴建立极坐标系，已知曲线的极坐标方程为，直线的参数方程为（为参数）．

（1）点在曲线上，且曲线在点处的切线与直线：垂直，求点的直角坐标；

（2）设直线与曲线有且只有一个公共点，求直线的斜率的取值范围．

【题目】某县为了帮助农户脱贫致富，鼓励农户利用荒地山坡种植果树，某农户考察了三种不同的果树苗、、．经过引种实验发现，引种树苗的自然成活率为，引种树苗、的自然成活率均为．

（1）任取树苗、、各一棵，估计自然成活的棵数为，求的分布列及其数学期望；

（2）将（1）中的数学期望取得最大值时的值作为种树苗自然成活的概率．该农户决定引种棵种树苗，引种后没有自然成活的树苗有的树苗可经过人工栽培技术处理，处理后成活的概率为，其余的树苗不能成活．

①求一棵种树苗最终成活的概率；

②若每棵树苗引种最终成活可获利元，不成活的每棵亏损元，该农户为了获利期望不低于万元，问至少要引种种树苗多少棵？

【题目】如图，在以、、、、、为顶点的五面体中，四边形为正方形，， ，．

（1）证明；

（2）求二面角的平面角的余弦值．

【题目】已知椭圆的左、右焦点分别为，右顶点为，且离心率为.

（1）求椭圆的标准方程；

（2）互相平行的两条直线分别过，且直线与椭圆交于两点，直线与椭圆交于，两点，若四边形的面积为，求直线的方程.

A.8B.9C.11D.12

【题目】已知两地相距，某船从地逆水到地，水速为，船在静水中的速度为．若船每小时的燃料费与其在静水中速度的平方成正比，当，每小时的燃料费为元，为了使全程燃料费最省，船的实际速度应为多少？

【题目】已知函数，.

（1）讨论函数的单调性；

（2）是否存在实数，使得“对任意恒成立”？若存在，求出的取值范围；若不存在，请说明理由.

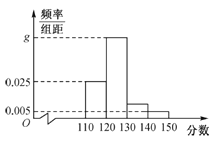
（1）求表中的值和频率分布直方图中的值；

（2）若同组中的每个数据用该组区间的中点值代替，试根据频率分布直方图求该学生高三年级数学考试分数的中位数和平均数，并对该学生自己在高考中的数学成绩进行预测.

(Ⅰ) 求数列{an}的通项公式；

(Ⅱ)若bn＝，且数列{bn}的前项和为Sn＝360，求的值.