
【题目】某县为了帮助农户脱贫致富,鼓励农户利用荒地山坡种植果树,某农户考察了三种不同的果树苗![]() 、
、![]() 、
、![]() .经过引种实验发现,引种树苗
.经过引种实验发现,引种树苗![]() 的自然成活率为
的自然成活率为![]() ,引种树苗
,引种树苗![]() 、
、![]() 的自然成活率均为
的自然成活率均为![]() .
.
(1)任取树苗![]() 、
、![]() 、
、![]() 各一棵,估计自然成活的棵数为
各一棵,估计自然成活的棵数为![]() ,求
,求![]() 的分布列及其数学期望;
的分布列及其数学期望;
(2)将(1)中的数学期望取得最大值时![]() 的值作为
的值作为![]() 种树苗自然成活的概率.该农户决定引种
种树苗自然成活的概率.该农户决定引种![]() 棵
棵![]() 种树苗,引种后没有自然成活的树苗有
种树苗,引种后没有自然成活的树苗有![]() 的树苗可经过人工栽培技术处理,处理后成活的概率为
的树苗可经过人工栽培技术处理,处理后成活的概率为![]() ,其余的树苗不能成活.
,其余的树苗不能成活.
①求一棵![]() 种树苗最终成活的概率;
种树苗最终成活的概率;
②若每棵树苗引种最终成活可获利![]() 元,不成活的每棵亏损
元,不成活的每棵亏损![]() 元,该农户为了获利期望不低于
元,该农户为了获利期望不低于![]() 万元,问至少要引种
万元,问至少要引种![]() 种树苗多少棵?
种树苗多少棵?
【答案】(1)分布列见解析,![]() ;(2)①
;(2)①![]() ;②
;②![]() 棵.
棵.
【解析】
(1)根据题意得出随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() ,计算出随机变量
,计算出随机变量![]() 在不同取值下的概率,可得出随机变量
在不同取值下的概率,可得出随机变量![]() 的分布列,进而可求得随机变量
的分布列,进而可求得随机变量![]() 的数学期望;
的数学期望;
(2)①由(1)知当![]() 时,
时,![]() 最大,然后分一棵
最大,然后分一棵![]() 种树苗自然成活和非自然成活两种情况,可求得所求事件的概率;
种树苗自然成活和非自然成活两种情况,可求得所求事件的概率;
②记![]() 为
为![]() 棵树苗的成活棵数,由题意可知
棵树苗的成活棵数,由题意可知![]() ,利用二项分布的期望公式得出
,利用二项分布的期望公式得出![]() ,根据题意得出关于
,根据题意得出关于![]() 的不等式,解出
的不等式,解出![]() 的取值范围即可得解.
的取值范围即可得解.
(1)依题意,![]() 的所有可能值为
的所有可能值为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以,随机变量![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
![]() ;
;
(2)由(1)知当![]() 时,
时,![]() 取得最大值.
取得最大值.
①一棵![]() 种树苗最终成活的概率为:
种树苗最终成活的概率为:![]() ,
,
②记![]() 为
为![]() 棵树苗的成活棵数,则
棵树苗的成活棵数,则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以该农户至少要种植![]() 棵树苗,才可获利不低于
棵树苗,才可获利不低于![]() 万元.
万元.


科目:高中数学 来源: 题型:
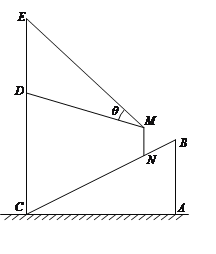
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高![]() 为
为![]() 米,它所占水平地面的长
米,它所占水平地面的长![]() 为
为![]() 米.该广告画最高点
米.该广告画最高点![]() 到地面的距离为
到地面的距离为![]() 米,最低点
米,最低点![]() 到地面距离
到地面距离![]() 米.假设某人眼睛到脚底的距离
米.假设某人眼睛到脚底的距离![]() 为
为![]() 米,他竖直站在此电梯上观看
米,他竖直站在此电梯上观看![]() 视角为
视角为![]() .
.
(Ⅰ)设此人到直线![]() 的距离为
的距离为![]() 米,试用含
米,试用含![]() 的表达式表示
的表达式表示![]() ;
;
(Ⅱ)此人到直线![]() 的距离为多少米时,视角
的距离为多少米时,视角![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问5分,(2)小问7分)
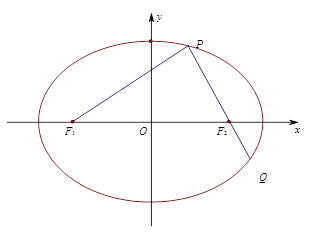
如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 过
过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]()
(1)若![]() ,求椭圆的标准方程
,求椭圆的标准方程
(2)若![]() 求椭圆的离心率
求椭圆的离心率![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求证:对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,都有
,都有![]() ;
;
(Ⅲ)若过点![]() 可作曲线
可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点P(-4,0)的动直线l与抛物线![]() 相交于D、E两点,已知当l的斜率为
相交于D、E两点,已知当l的斜率为![]() 时,
时,![]() .
.
(1)求抛物线C的方程;
(2)设![]() 的中垂线在
的中垂线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个线性回归方程![]() ,变量x增加1个单位时,y平均增加5个单位;
,变量x增加1个单位时,y平均增加5个单位;
③设具有相关关系的两个变量x,y的相关系数为r,则|r|越接近于0,x和y之间的线性相关程度越强;
④在一个2×2列联表中,由计算得K2的值,则K2的值越大,判断两个变量间有关联的把握就越大.
以上错误结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中重要的一部分,其中大学生更是频频使用网络外卖服务.![]() 市教育主管部门为掌握网络外卖在该市各大学的发展情况,在某月从该市大学生中随机调查了
市教育主管部门为掌握网络外卖在该市各大学的发展情况,在某月从该市大学生中随机调查了![]() 人,并将这
人,并将这![]() 人在本月的网络外卖的消费金额制成如下频数分布表(已知每人每月网络外卖消费金额不超过
人在本月的网络外卖的消费金额制成如下频数分布表(已知每人每月网络外卖消费金额不超过![]() 元):
元):
消费金额(单位:百元) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
![]() 由频数分布表可以认为,该市大学生网络外卖消费金额
由频数分布表可以认为,该市大学生网络外卖消费金额![]() (单位:元)近似地服从正态分布
(单位:元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值,
(每组数据取区间的中点值,![]() ).现从该市任取
).现从该市任取![]() 名大学生,记其中网络外卖消费金额恰在
名大学生,记其中网络外卖消费金额恰在![]() 元至
元至![]() 元之间的人数为
元之间的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
![]()
![]() 市某大学后勤部为鼓励大学生在食堂消费,特地给参与本次问卷调查的大学生每人发放价值
市某大学后勤部为鼓励大学生在食堂消费,特地给参与本次问卷调查的大学生每人发放价值![]() 元的饭卡,并推出一档“勇闯关,送大奖”的活动.规则是:在某张方格图上标有第
元的饭卡,并推出一档“勇闯关,送大奖”的活动.规则是:在某张方格图上标有第![]() 格、第
格、第![]() 格、第
格、第![]() 格、…、第
格、…、第![]() 格共
格共![]() 个方格.棋子开始在第
个方格.棋子开始在第![]() 格,然后掷一枚均匀的硬币(已知硬币出现正、反面的概率都是
格,然后掷一枚均匀的硬币(已知硬币出现正、反面的概率都是![]() ,其中
,其中![]() ),若掷出正面,将棋子向前移动一格(从
),若掷出正面,将棋子向前移动一格(从![]() 到
到![]() ),若掷出反面,则将棋子向前移动两格(从
),若掷出反面,则将棋子向前移动两格(从![]() 到
到![]() ).重复多次,若这枚棋子最终停在第
).重复多次,若这枚棋子最终停在第![]() 格,则认为“闯关成功”,并赠送
格,则认为“闯关成功”,并赠送![]() 元充值饭卡;若这枚棋子最终停在第
元充值饭卡;若这枚棋子最终停在第![]() 格,则认为“闯关失败”,不再获得其他奖励,活动结束.
格,则认为“闯关失败”,不再获得其他奖励,活动结束.
①设棋子移到第![]() 格的概率为
格的概率为![]() ,求证:当
,求证:当![]() 时,
时,![]() 是等比数列;
是等比数列;
②若某大学生参与这档“闯关游戏”,试比较该大学生闯关成功与闯关失败的概率大小,并说明理由.
参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com