【题目】如图，是以为直径的半圆上异于点的点，矩形所在的平面垂直于该半圆所在平面，且

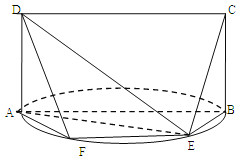
(Ⅰ)求证：；

(Ⅱ)设平面与半圆弧的另一个交点为,

①求证：//;

②若，求三棱锥E-ADF的体积．

【题目】如图1， 在直角梯形中， ， ， ， 为线段的中点. 将沿折起，使平面 平面，得到几何体，如图2所示.

（1）求证: 平面；

（2）求二面角的余弦值.

【题目】已知函数（其中是自然对数的底数）

（1）若在R上单调递增，求正数a的取值范围；

（2）若f（x）在处导数相等，证明：；

（3）当时，证明：对于任意，若，则直线与曲线有唯一公共点（注：当时，直线与曲线的交点在y轴两侧）.

①将一组数据中的每一个数据都加上或减去同一个常数后，方差不变；

②设有一个线性回归方程，变量x增加1个单位时，y平均增加5个单位；

③设具有相关关系的两个变量x，y的相关系数为r，则|r|越接近于0，x和y之间的线性相关程度越强；

④在一个2×2列联表中，由计算得K2的值，则K2的值越大，判断两个变量间有关联的把握就越大．

以上错误结论的个数为(　　)

A. 0 B. 1 C. 2 D. 3

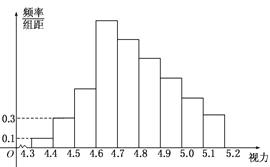
A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83

A.76,63,17,00B.16,00,02,30C.17,00,02,25D.17,00,02,07

A.充分不必要条件B.必要不充分条件

C.充分必要条件D.既不充分也不必要条件

【题目】在直角坐标系中，直线的参数方程为 (为参数)，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）为曲线的动点，点在线段上，且满足，求点的轨迹的直角坐标方程；

（2）设点的极坐标为，点在曲线上，求面积的最大值及此时点坐标．

（3）设直线与曲线交于点，若点的坐标为，求的值．

【题目】在直角坐标系中，直线经过点，其倾斜角为．以原点为极点，以轴非负半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系．设曲线的极坐标方程为．

（1）写出直线的参数方程，若直线与曲线有公共点，求的取值范围．

（2）设为曲线上任意一点，求的取值范围．

【题目】已知函数，．

求函数的单调区间；

当时，若在区间上恒成立，求的取值范围．