【题目】如图，半径为2的切直线MN于点P，射线PK从PN出发绕点P逆时针方向旋转到PM，旋转过程中，PK交于点Q，设为x，弓形PmQ的面积为，那么的图象大致是　　

A. B.

C. D.

【题目】已知函数，.（为自然对数的底数）

（1）设；

①若函数在处的切线过点，求的值；

②当时，若函数在上没有零点，求的取值范围.

（2）设函数，且，求证：当时，.

【题目】设椭圆的一个顶点与抛物线的焦点重合，，分别是椭圆的左、右焦点，离心率，过椭圆右焦点的直线与椭圆交于，两点．

（Ⅰ）求椭圆的方程；

（Ⅱ）是否存在直线，使得，若存在，求出直线的方程；若不存在，说明理由；

（Ⅲ）设点是一个动点，若直线的斜率存在，且为中点，，求实数的取值范围．

【题目】如图，在四棱锥中，平面．底面是菱形，．

（Ⅰ）求证：直线平面；

（Ⅱ）求直线与平面所成角的正切值；

（Ⅲ）已知在线段上，且，求二面角的余弦值．

方式一：周一到周五每天培训1小时，周日测试

方式二：周六一天培训4小时，周日测试

公司有多个班组，每个班组60人，现任选两组记为甲组、乙组先培训；甲组选方式一，乙组选方式二，并记录每周培训后测试达标的人数如表：

用方式一与方式二进行培训，分别估计员工受训的平均时间精确到，并据此判断哪种培训方式效率更高？

在甲乙两组中，从第三周培训后达标的员工中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求这2人中至少有1人来自甲组的概率．

用分别表示甲、乙两班抽取的5名学生学分的方差，计算两个班学分的方差．得______，并由此可判断成绩更稳定的班级是______班．

在直角坐标系中，曲线的参数方程为（是参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）求曲线的极坐标方程和曲线的直角坐标方程；

（2）若射线 与曲线交于，两点，与曲线交于，两点，求取最大值时的值

【题目】已知函数 .

（1）若，判断函数的单调性；

（2）讨论函数的极值，并说明理由.

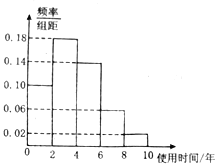
（1）若在该市场随机选取1个2018年成交的二手电脑，求其使用时间在上的概率；

（2）根据电脑交易市场往年的数据，得到如图所示的散点图及一些统计量的值，其中（单位：年）表示折旧电脑的使用时间，（单位：百元）表示相应的折旧电脑的平均交易价格.

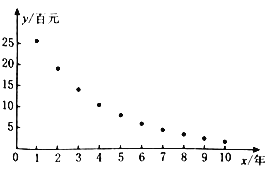
由散点图判断，可采用作为该交易市场折旧电脑平均交易价格与使用年限的回归方程，若，，选用如下参考数据，求关于的回归方程，并预测在区间（用时间组的区间中点值代表该组的值）上折旧电脑的价格.

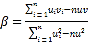附：参考公式：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为：，.参考数据：，，，，.

（Ⅰ）当m=1时，求不等式f（x）≥1的解集；

（Ⅱ）若x∈R，t∈R，使得f（x）+|t-1|＜|t+1|，求实数m的取值范围．