
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,离心率
的左、右焦点,离心率![]() ,过椭圆
,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
(Ⅲ)设点![]() 是一个动点,若直线
是一个动点,若直线![]() 的斜率存在,且
的斜率存在,且![]() 为
为![]() 中点,
中点,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)答案见解析;(Ⅲ)
;(Ⅱ)答案见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由题意求得a,b,c的值即可确定椭圆方程;
(Ⅱ)联立直线方程与椭圆方程,结合韦达定理和向量的坐标运算法则求得直线的斜率即可确定直线方程;
(Ⅲ)由题意结合点差法得到![]() 的表达式,结合其表达式求解取值范围即可.
的表达式,结合其表达式求解取值范围即可.
(Ⅰ)抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,故
,故![]() ,
,
结合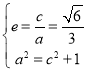 可得:
可得: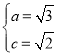 ,故椭圆方程为:
,故椭圆方程为:![]() .
.
(Ⅱ)很明显直线的斜率存在,设![]() ,
,
假设存在满足题意的直线方程:![]() ,
,
与椭圆方程![]() 联立可得:
联立可得:![]() ,
,
则![]() ,
,
则:![]()
![]() ,
,
结合题意和韦达定理有:![]() ,
,
解得:![]() ,即存在满足题意的直线方程:
,即存在满足题意的直线方程:![]() .
.
(Ⅲ)设![]() ,设直线AB的方程为
,设直线AB的方程为![]() ,
,
由于:![]() ,
,
两式作差整理变形可得:![]() ,
,
即:![]() . ①
. ①
又![]() ②
②
![]() ③
③
①×②可得:![]() ④
④
④代入③可得:![]() ⑤
⑤
④⑤代入①整理可得: ,
,
![]() ,据此可得:
,据此可得:![]() ,
,
从而![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且短轴长为
,且短轴长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,设点
,设点![]() 为第四象限内一点且在椭圆
为第四象限内一点且在椭圆![]() 上(点
上(点![]() 不在直线
不在直线![]() 上),点
上),点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() .设
.设![]() 为坐标原点,判断直线
为坐标原点,判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若对任意
时,若对任意![]() 均有
均有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)设直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() ,其中
,其中![]() .
.
①求证:![]() ;
;
②当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx-1,当x=-2时有极值,且在x=-1处的切线的斜率为-3.
(1)求函数f(x)的解析式.
(2)求函数f(x)在区间[-1,2]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
(1)求E的方程;
(2)若点A,B是E上的两个动点,O为坐标原点,且![]() ,求证:直线AB恒过定点.
,求证:直线AB恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】立德中学和树人中学各派一名学生组成一个联队参加一项智力竞赛,这个智力竞赛一共两轮,在每一轮中,两名同学各回答一次题目,已知,立德中学派出的学生每轮中答对问题的概率都是![]() ,树人中学派出的学生每轮中答对问题的概率都是
,树人中学派出的学生每轮中答对问题的概率都是![]() ;每轮中,两位同学答对与否互不影响,各论结果亦互不影响,求:
;每轮中,两位同学答对与否互不影响,各论结果亦互不影响,求:
(Ⅰ)两轮比赛后,立德中学的学生恰比树人中学的学生答对题目的个数多![]() 个的概率;
个的概率;
(Ⅱ)两轮比赛后,记![]() 为这两名同学一共答对的题目数,求随机变量
为这两名同学一共答对的题目数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,上顶点为
,上顶点为![]() ,右焦点为
,右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 为
为![]() 轴上的两个动点,且
轴上的两个动点,且![]() ,直线
,直线![]() 和
和![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求![]() 的面积最小值;
的面积最小值;
(ⅱ)证明:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)

(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com