【题目】已知函数，其中为自然对数的底数，．

（1）若恰有两个零点，求实数的取值范围；

（2）若，且，求证：．

【题目】已知点在圆：上运动，点在轴上的投影为，动点满足．

（1）求动点的轨迹的方程；

（2）过点的动直线与曲线交于、两点，问：在轴上是否存在定点使得的值为定值？若存在，求出定点的坐标及该定值；若不存在，请说明理由．

【题目】大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行月薪情况的问卷调查，经统计发现，他们的月薪收入在3000元到10000元之间，具体统计数据如表：

（1）经统计发现，该大学2018届的大学本科毕业生月薪（单位：百元）近似地服从正态分布，其中近似为样本平均数（每组数据取区间的中点值）．若落在区间的左侧，则可认为该大学本科生属“就业不理想”的学生，学校将联系本人，咨询月薪过低的原因，为以后的毕业生就业提供更好的指导意见．现该校2018届大学本科毕业生张茗的月薪为3600元，试判断张茗是否属于“就业不理想”的学生；

（2）①将样本的频率视为总体的概率，若大学领导决定从大学2018届所有本毕业生中任意选取5人前去探访，记这5人中月薪不低于8000元的人数为，求的数学期望与方差；

②在（1）的条件下，中国移动赞助了大学的这次社会调查活动，并为这次参与调查的大学本科毕业生制定了赠送话费的活动，赠送方式为：月薪低于的获赠两次随机话费，月薪不低于的获赠一次随机话费；每次赠送的话费及对应的概率分别为：

则张茗预期获得的话费为多少元？（结果保留整数）

【题目】如图，点在以为直径的上运动，平面，且，点、分别是、的中点．

（1）求证：平面平面；

（2）若，求平面与平面所成锐二面角的余弦值．

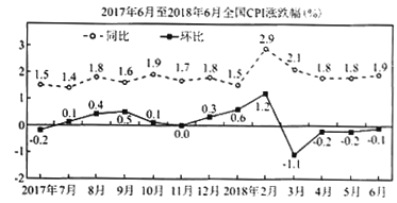
A.2017年8月与同年12月相比较，8月环比更大

B.2018年1月至6月各月与2017年同期相比较，CPI只涨不跌

C.2018年1月至2018年6月CPI有涨有跌

D.2018年3月以来，CPI在缓慢增长

【题目】已知函数，，.

（1）若函数在上是单调函数，求实数m的取值范围；

（2）当时，

（i）求函数在点处的切线方程；

（ii）若对任意，不等式恒成立，求实数a的取值范围.

【题目】已知椭圆C：（）的短轴长为，离心率为.

（1）求椭圆C的标准方程；

（2）设M，N分别为椭圆C的左、右顶点，过点且不与x轴重合的直线与椭圆C相交于A，B两点是否存在实数t（），使得直线：与直线的交点P满足P，A，M三点共线？若存在，求出的方程；若不存在，请说明理由.

【题目】如图，在四棱锥中，底面为直角梯形，，为等边三角形，，是的中点.

（1）证明：平面平面；

（2）求直线与平面所成角的正弦值.