
科目: 来源: 题型:
【题目】已知椭圆![]() 的左右两焦点分别为
的左右两焦点分别为![]() 、
、![]() .
.
(1)若矩形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 均在
均在![]() 上,求该矩形绕
上,求该矩形绕![]() 轴旋转一周所得圆柱侧面积
轴旋转一周所得圆柱侧面积![]() 的取值范围;
的取值范围;
(2)设斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() (
(![]() ),求证:
),求证:![]() ;
;
(3)过![]() 上一动点
上一动点![]() 作直线
作直线![]() ,其中
,其中![]() ,过
,过![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:阳马指底面为矩形,一侧棱垂直于底面的四棱锥,堑堵指底面是直角三角形,且侧棱垂直于底面的三棱柱.
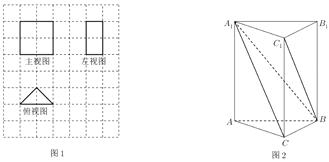
(1)某堑堵的三视图,如图1,网格中的每个小正方形的边长为1,求该堑堵的体积;
(2)在堑堵![]() 中,如图2,
中,如图2,![]() ,若
,若![]() ,当阳马
,当阳马![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】上海地铁四通八达,给市民出行带来便利,已知某条线路运行时,地铁的发车时间间隔![]() (单位:分字)满足:
(单位:分字)满足:![]() ,
,![]() ,经测算,地铁载客量
,经测算,地铁载客量![]() 与发车时间间隔
与发车时间间隔![]() 满足
满足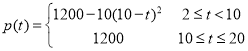 ,其中
,其中![]() .
.
(1)请你说明![]() 的实际意义;
的实际意义;
(2)若该线路每分钟的净收益为![]() (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?并求最大净收益.
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?并求最大净收益.
查看答案和解析>>
科目: 来源: 题型:
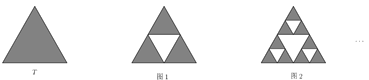
【题目】对于正三角形![]() ,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设
,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设![]() 是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设
是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设![]() 是第
是第![]() 次挖去的小三角形面积之和(如
次挖去的小三角形面积之和(如![]() 是第1次挖去的中间小三角形面积,
是第1次挖去的中间小三角形面积,![]() 是第2次挖去的三个小三角形面积之和),
是第2次挖去的三个小三角形面积之和),![]() 是前
是前![]() 次挖去的所有三角形的面积之和,则
次挖去的所有三角形的面积之和,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如![]() ,在不超过13的素数中,随机选取两个不同的数,其和为偶数的概率是________(用分数表示)
,在不超过13的素数中,随机选取两个不同的数,其和为偶数的概率是________(用分数表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产x万件,需另投入流动成本C(x)万元,当年产量小于7万件时,C(x)=![]() x2+2x(万元);当年产量不小于7万件时,C(x)=6x+1nx+
x2+2x(万元);当年产量不小于7万件时,C(x)=6x+1nx+![]() ﹣17(万元).已知每件产品售价为6元,假若该同学生产的产M当年全部售完.
﹣17(万元).已知每件产品售价为6元,假若该同学生产的产M当年全部售完.
(1)写出年利润P(x)(万元)关于年产量x(万件)的函数解析式;(注:年利润=年销售收人﹣固定成本﹣流动成本
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?(取e3≈20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com