
科目: 来源: 题型:
【题目】设函数![]() (a,b
(a,b![]() R).
R).
(1)当b=﹣1时,函数![]() 有两个极值,求a的取值范围;
有两个极值,求a的取值范围;
(2)当a+b=1时,函数![]() 的最小值为2,求a的值;
的最小值为2,求a的值;
(3)对任意给定的正实数a,b,证明:存在实数![]() ,当
,当![]() 时,
时,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,己知圆C经过点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),且与直线
),且与直线![]() 相切.
相切.
(1)求圆C的方程;
(2)设P是直线l:x=4上的任意一点,过点P作圆C的切线,切点为M,N.
①求证:直线MN过定点(记为Q);
②设直线PQ与圆C交于点A,B,与y轴交于点D.若![]() ,
,![]() ,求+的值.
,求+的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某地有一块半径为R的扇形AOB公园,其中O为扇形所在圆的圆心,AOB=![]() ,OA,OB,
,OA,OB,![]() 为公园原有道路.为满足市民观赏和健身的需要,市政部门拟在
为公园原有道路.为满足市民观赏和健身的需要,市政部门拟在![]() 上选取一点M,新建道路OM及与OA平行的道路MN(点N在线段OB上),设AOM=
上选取一点M,新建道路OM及与OA平行的道路MN(点N在线段OB上),设AOM=![]() .
.

(1)如何设计,才能使市民从点O出发沿道路OM,MN行走至点N所经过的路径最长?请说明理由;
(2)如何设计,才能使市民从点A出发沿道路![]() ,MN行走至点N所经过的路径最长?请说明理由.
,MN行走至点N所经过的路径最长?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 以抛物线
以抛物线![]() 的焦点为顶点,且离心率为
的焦点为顶点,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,
点,![]() 是椭圆
是椭圆![]() 上一点且满足
上一点且满足![]() (其中
(其中![]() 为坐标原点),试问在
为坐标原点),试问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标及
的坐标及![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.
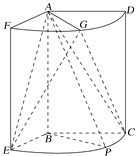
(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系中有16个格点(i,j),其中0≤i≤3,0≤j≤3.若在这16个点中任取n个点,这n个点中总存在4个点,这4个点是一个正方形的顶点,求n的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系![]() 中,曲线
中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设
,设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 、
、![]() .以
.以![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴的正半轴建立直角坐标系
轴的正半轴建立直角坐标系![]() .
.
(1)求![]() 的直角坐标方程与点
的直角坐标方程与点![]() 的直角坐标;
的直角坐标;
(2)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com