
【题目】在平面直角坐标系xOy中,己知圆C经过点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),且与直线
),且与直线![]() 相切.
相切.
(1)求圆C的方程;
(2)设P是直线l:x=4上的任意一点,过点P作圆C的切线,切点为M,N.
①求证:直线MN过定点(记为Q);
②设直线PQ与圆C交于点A,B,与y轴交于点D.若![]() ,
,![]() ,求+的值.
,求+的值.
【答案】(1)![]() (2)①证明见解析;②
(2)①证明见解析;②![]()
【解析】
(1)设圆C的方程为![]() ,由此得
,由此得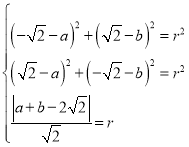 ,解出即可;
,解出即可;
(2)①设P(4,![]() ),由题意P,M,N,C在以PC为直径的圆
),由题意P,M,N,C在以PC为直径的圆![]() 上,两圆方程作差可得直线MN的方程为
上,两圆方程作差可得直线MN的方程为![]() ,由直线系方程即可求出定点;
,由直线系方程即可求出定点;
②由①得Q(1,0),设直线PQ的方程为![]() ,则D(0,﹣k),设A(
,则D(0,﹣k),设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),联立直线与圆的方程消元,由韦达定理可得
),联立直线与圆的方程消元,由韦达定理可得 ,根据题意可得到
,根据题意可得到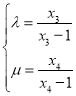 ,代入后化简求值即可.
,代入后化简求值即可.
解:(1)设圆C的方程为![]() ,
,
由题意可得,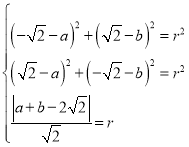 ,
,
解得![]() ,
,![]() ,
,![]() ,
,
∴圆C的方程为![]() ;
;
(2)①设P(4,![]() ),
),
∵PM,PN是圆C的两条切线,
∴PM⊥MC,PN⊥NC,
∴P,M,N,C在以PC为直径的圆上,
∴该圆上任意一点![]() 满足
满足![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴该圆方程为![]() ,
,
由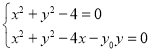 作差可得公共弦所在直线MN的方程为
作差可得公共弦所在直线MN的方程为![]() ,
,
∴直线MN过定点(1,0);
②由①可得Q(1,0),设直线PQ的方程为![]() ,则D(0,﹣k),
,则D(0,﹣k),
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
由![]() 得
得![]() ,
,
∴ ,
,
由![]() ,
,![]() ,得
,得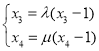 ,即
,即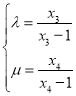 ,
,
∴![]()
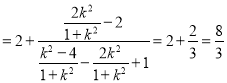 .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F,直线l与C交于M,N两点.
的右焦点为F,直线l与C交于M,N两点.
(1)若l过点F,点M,N到直线y=2的距离分别为d1,d2,且![]() ,求l的方程;
,求l的方程;
(2)若点M的坐标为(0,1),直线m过点M交C于另一点N′,当直线l与m的斜率之和为2时,证明:直线NN′过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 、
、![]() (如图②).在折起的过程中,则下列表述:
(如图②).在折起的过程中,则下列表述:

①![]() 平面
平面![]() ;
;
②四点![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.其中正确的是__________.
可能垂直.其中正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.
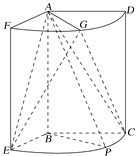
(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为![]() ,则f(
,则f(![]() )的值为( )
)的值为( )
A.﹣1B.1C.![]() .D.
.D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() ,设数列
,设数列![]() 、
、![]() 的前
的前![]() 项和分别为
项和分别为![]() 和
和![]() .
.
(1)若数列![]() 是等差数列,求
是等差数列,求![]() 和
和![]() ;
;
(2)若数列![]() 是公比为2的等比数列.
是公比为2的等比数列.
①求![]() ;
;
②是否存在实数![]() ,使
,使![]() 对任意自然数
对任意自然数![]() 都成立?若存在,求
都成立?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com