
科目: 来源: 题型:
【题目】2020年是全面建成小康社会目标实现之年,也是全面打赢脱贫攻坚战收官之年.某乡镇在2014年通过精准识别确定建档立卡的贫困户共有500户,结合当地实际情况采取多项精准扶贫措施,每年新脱贫户数如下表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
脱贫户数 | 55 | 68 | 80 | 92 | 100 |
(1)根据2015-2019年的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测到2020年底该乡镇500户贫困户是否能全部脱贫;
,并预测到2020年底该乡镇500户贫困户是否能全部脱贫;
(2)2019年的新脱贫户中有20户五保户,20户低保户,60户扶贫户.该乡镇某干部打算按照分层抽样的方法对2019年新脱贫户中的5户进行回访,了解生产生活、帮扶工作开展情况.为防止这些脱贫户再度返贫,随机抽取这5户中的2户进行每月跟踪帮扶,求抽取的2户不都是扶贫户的概率.
参考公式: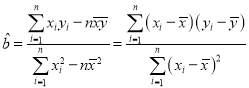 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】意大利数学家斐波那契的《算经》中记载了一个有趣的问题:已知一对兔子每个月可以生一对兔子,而一对兔子出生后在第二个月就开始生小兔子.假如没有发生死亡现象,那么兔子对数依次为:1,1,2,3,5,8,13,21,34,55,89,144……,这就是著名的斐波那契数列,它的递推公式是![]() ,其中
,其中![]() ,
,![]() .若从该数列的前120项中随机地抽取一个数,则这个数是奇数的概率为( )
.若从该数列的前120项中随机地抽取一个数,则这个数是奇数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.23 | 4.70 | 3.72 | 3.12 | 2.42 |
倒闭企业所占比例 | 21.8% | 19.6% | 15.5% | 13.0% | 10.1% |
根据上表,给出两种回归模型:
模型①:建立曲线型回归模型![]() ,求得回归方程为
,求得回归方程为![]() ;
;
模型②:建立线性回归模型![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测
,并选择拟合精度更高、更可靠的模型,预测![]() 年成立的企业中倒闭企业所占比例(结果保留整数).
年成立的企业中倒闭企业所占比例(结果保留整数).
回归模型 | 模型① | 模型② |
回归方程 |
|
|
|
|
参考公式: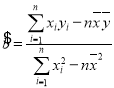 ,
,![]() ;
;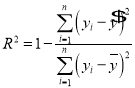 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 只有一个公共点,点
只有一个公共点,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程;
的方程;
(2)①若![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
②若![]() 是抛物线
是抛物线![]() 上与原点不重合的定点,且
上与原点不重合的定点,且![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为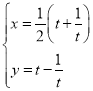 (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系.
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)写出曲线C的普通方程和极坐标方程;
(Ⅱ)M,N为曲线C.上两点,若OM⊥ON,求|MN|的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为筛查在人群中传染的某种病毒,现有两种检测方法:
(1)抗体检测法:每个个体独立检测,每一次检测成本为80元,每个个体收取检测费为100元.
(2)核酸检测法:先合并个体,其操作方法是:当个体不超过10个时,把所有个体合并在一起进行检测.
当个体超过10个时,每10个个体为一组进行检测.若该组检测结果为阴性(正常),则只需检测一次;若该组检测结果为阳性(不正常),则需再对每个个体按核酸检测法重新独立检测,共需检测k+1次(k为该组个体数,1≤k≤10,k∈N*).每一次检测成本为160元.假设在接受检测的个体中,每个个体的检测结果是阳性还是阴性相互独立,且每个个体是阳性结果的概率均为p(0<p<1).
(Ⅰ)现有100个个体采取抗体检测法,求其中恰有一个检测出为阳性的概率;
(Ⅱ)因大多数人群筛查出现阳性的概率很低,且政府就核酸检测法给子检测机构一定的补贴,故检测机构推出组团选择核酸检测优惠政策如下:无论是检测一次还是k+1次,每组所有个体共收费700元(少于10个个体的组收费金额不变).已知某企业现有员工107人,准备进行全员检测,拟准备9000元检测费,由于时间和设备条件的限制,采用核酸检测法合并个体的组数不得高于参加采用抗体检测法人数,请设计一个合理的的检测安排方案;
(Ⅲ)设![]() ,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
,现有n(n∈N*且2≤n≤10)个个体,若出于成本考虑,仅采用一种检测方法,试问检测机构应采用哪种检测方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
查看答案和解析>>
科目: 来源: 题型:
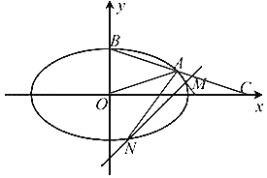
【题目】如图所示,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 上位于第一象限上的点,
上位于第一象限上的点,![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 过椭圆
过椭圆![]() 的右焦点,且与椭圆
的右焦点,且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 在直线
在直线![]() 的同侧),若
的同侧),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com