
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,求证:
,求证:![]() ..
..
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)由题意![]() 的定义域为
的定义域为![]() ,求导得
,求导得![]() ,由题意比较
,由题意比较![]() 与
与![]() 的大小,分类讨论即可求出函数的单调性;
的大小,分类讨论即可求出函数的单调性;
(2)由题意,![]()
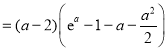 ,令
,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,再结合导数依次求得函数
,再结合导数依次求得函数![]() 的单调性与最值,由此可证.
的单调性与最值,由此可证.
解:(1)由题意![]() 的定义域为
的定义域为![]() ,
,
![]()
![]() ,
,
①若![]() ,由
,由![]() 得,
得,![]() ,解得
,解得![]() ,由
,由![]() ,得
,得![]() ,则
,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②若![]() ,由
,由![]() ,得
,得![]() ,或
,或![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得,
得,![]() ,解得
,解得![]() ,由
,由![]() ,得
,得![]() ,或
,或![]() ,则
,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() 得,
得,![]() ,解得
,解得![]() ,由
,由![]() ,得
,得![]() ,或
,或![]() ,则
,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
综上:当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
(2)由题意,![]()
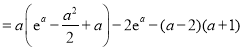
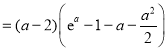 ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
![]() ,而
,而![]() ,
,
![]() ,
,
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】现有某种不透明充气包装的袋装零食,每袋零食附赠玩具A,B,C中的一个.对某零售店售出的100袋零食中附赠的玩具类型进行追踪调查,得到以下数据:
BBABC ACABA AAABC BABAA CAAAB
ABCCC BCBBC CABCA BACAB BCBCB
BCCCA BCCAA BCCCB ACCBB BACAB
ACCAB BBBAA CABCA BCBBC CABCA
(1)能否认为购买一袋该零食,获得玩具A,B,C的概率相同?请说明理由;
(2)假设每袋零食随机附赠玩具A,B,C是等可能的,某人一次性购买该零食3袋,求他能从这3袋零食中集齐玩具A,B及C的概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为_____.
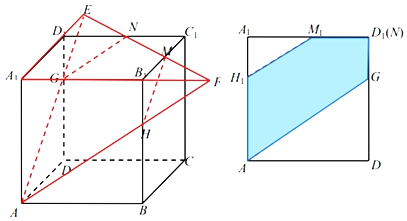
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 只有一个公共点,点
只有一个公共点,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程;
的方程;
(2)①若![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
②若![]() 是抛物线
是抛物线![]() 上与原点不重合的定点,且
上与原点不重合的定点,且![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据国家统计局数据:2000年,2018年我国GDP(国内生产总值)分别为10万亿,90万亿.2000年与2018年国内生产总值中第一产业、第二产业、第三产生的比例如图,则对比2000年与2018年的数据,下列说法错误的是( )
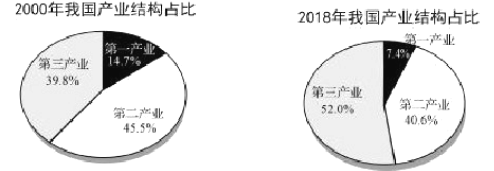
A.第一产业占比减少了约一半B.第二产业占比变化最小
C.第三产业生产总值增长了约11倍D.第一产业生产总值变化量最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数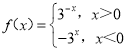 ,若
,若![]() ,b=f(log24.2),c=f(20.7),则a,b,c的大小关系为( )
,b=f(log24.2),c=f(20.7),则a,b,c的大小关系为( )
A.a<b<cB.b<a<cC.c<a<bD.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小相同的5个小球,编号分别为0,1,2,3,4,现从中随机地摸一个球,记下编号后放回,连摸3次,若摸出的3个小球的最大编号与最小编号之差为2,则共有________种不同的摸球方法(用数字作答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com