【题目】冠状病毒是一个大型病毒家族，已知可引起感冒以及中东呼吸综合征和严重急性呼吸综合征等较严重疾病. 而今年出现的新型冠状病毒是以前从未在人体中发现的冠状病毒新毒株. 人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等. 在较严重病例中感染可导致肺奖、严重急性呼吸综合征、贤衰竭，甚至死亡.核酸检测是诊断新冠肺炎的重要依据，首先取病人的唾液或咽拭子的样本，再提取唾液或咽拭子样本里的遗传物质，如果有病毒，样本检测会呈现阳性，否则为阴性. 根据统计发现，疑似病例核酸检测呈阳性的概率为，现有例疑似病例，分别对其取样、检测，多个样本检测时，既可以逐个化验，也可以将若干个样本混合在一起化验，混合样本中只要有病毒，则混合样本化验结果就会呈阳性，若混合样本呈阳性，则将该组中各个样本再逐个化验；若混合样本呈阴性，则该组各个样本均为阴性.现有以下三种方案:

方案一：逐个化验；

方案二：四个样本混在一起化验；

方案三: 平均分成两组化验.

在新冠肺炎爆发初期，由于检查能力不足，化检次数的期望值越小，则方案越“优”.

（1）若，求个疑似病例样本混合化验结果为阳性的概率；

（2）若，现将该例疑似病例样本进行化验，请问：方案一、二、 三中哪个最“优”?

（3）若对例疑似病例样本进行化验，且“方案二”比“方案一”更“优”，求的取值范围.

【题目】在平面直角坐标系中，为坐标原点，，，已知是以为底边，且边平行于轴的等腰三角形.

（1）求动点的轨迹的方程；

（2）已知直线交轴于点，且与曲线相切于点，点在曲线上，且直线轴，点关于点的对称点为点，试判断点、、三点是否共线，并说明理由.

【题目】如图，在直角中，，，，、分别是、上一点，且满足平分，，以为折痕将折起，使点到达点的位置，且平面平面.

（1）证明：；

（2）求二面角的正弦值.

【题目】“众志成城，抗击疫情，一方有难，八方支援”，在此次抗击疫情过程中，各省市都派出援鄂医疗队. 假设汕头市选派名主任医生，名护士，组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援，每个小组包括名主任医生和名护士，则不同的分配方案有（ ）

A.种B.种C.种D.种

【题目】在直角坐标系中，曲线的参数方程为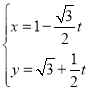（为参数），以原点为极点，以x轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）求曲线的极坐标方程与曲线的直角坐标方程；

（2）设、为曲线上位于第一，二象限的两个动点，且，射线，交曲线分别于点，.求面积的最小值，并求此时四边形的面积.

【题目】已知圆，动点，线段QF与圆F相交于点P，线段PQ的长度与点Q到y轴的距离相等．

（Ⅰ）求动点Q的轨迹W的方程；

（Ⅱ）过点作两条互相垂直的直线与W的交点分别是M和N（M在N的上方，A，M，N为不同的三点），求向量在y轴正方向上的投影的取值范围．

【题目】设函数．

（Ⅰ）若当时取得极值，求a的值及的单调区间；

（Ⅱ）若存在两个极值点，，证明：．

【题目】某快递公司招聘快递骑手，该公司提供了两种日工资方案：方案（1）规定每日底薪50元，快递骑手每完成一单业务提成3元：方案（2）规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元．该快递公司记录了每天骑手的人均业务量．现随机抽取100天的数据，将样本数据分为七组，整理得到如图所示的频率分布直方图．

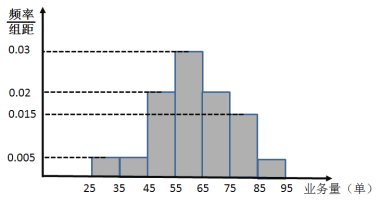
（Ⅰ）随机选取一天，估计这一天该快递公司的骑手的人均日快递业务量不少于65单的概率；

（Ⅱ）若骑手甲、乙、丙选择了日工资方案（1），丁、戊选择了日工资方案（2）．现从上述5名骑手中随机选取2人，求至少有1名骑手选择方案（2）的概率；

（Ⅲ）若仅从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由（同组中的每个数据用该组区间的中点值代替）

【题目】在直角梯形ABCD中（如图1），，，，，，点E在CD上，且，将沿AE折起，使得平面平面ABCE（如图2），G为AE中点．

（Ⅰ）求四棱锥的体积；

（Ⅱ）在线段BD上是否存在点P，使得平面ADE？若存在，求的值；若不存在，请说明理由．

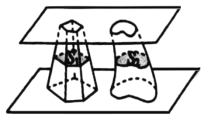
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”．其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等，如图，夹在两个平行平面之间的两个几何体的体积分别为，，被平行于这两个平面的任意平面截得的两个截面面积分别为、，则“、不总相等”是“，不相等”的（ ）

A.充分而不必要条件B.必要而不充分条件

C.充分必要条件D.既不充分也不必要条件