
科目: 来源: 题型:
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
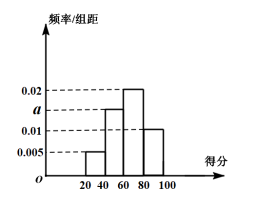
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 | a | 24 | b |
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】以直角坐标系![]() 的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线
的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线![]() (
(![]() 为参数)上每一点的横坐标变为原来的
为参数)上每一点的横坐标变为原来的![]() (纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为
(纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,与x轴交于点P,线段AB的中点为M,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某基地蔬菜大棚采用无土栽培方式种植各类蔬菜.根据过去50周的资料显示,该基地周光照量![]() (小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量![]() (千克)与使用某种液体肥料的质量
(千克)与使用某种液体肥料的质量![]() (千克)之间的关系如图所示.
(千克)之间的关系如图所示.
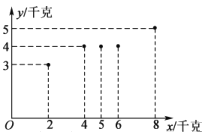
(1)依据上图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以频率作为概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数公式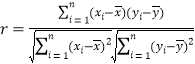 ,
,
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆M:![]() ,直线l:
,直线l:![]() (
(![]() )过定点N,点P是圆M上的任意一点,线段
)过定点N,点P是圆M上的任意一点,线段![]() 的垂直平分线和
的垂直平分线和![]() 相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线C.
相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)直线l交C于A,B两点,D,B关于x轴对称,直线![]() 与x轴交于点E,且点D为线段
与x轴交于点E,且点D为线段![]() 的中点,求直线l的方程.
的中点,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是由边长为4的正六边形![]() ,矩形
,矩形![]() ,组成的一个平面图形,将其沿
,组成的一个平面图形,将其沿![]() ,
,![]() 折起得几何体
折起得几何体![]() ,使得
,使得![]() ,且平面
,且平面![]() 平面
平面![]() ,如图2.
,如图2.
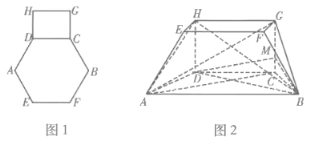
(1)证明:图2中,平面![]() 平面
平面![]() ;
;
(2)设点M为图2中线段![]() 上一点,且
上一点,且![]() ,若直线
,若直线![]() 平面
平面![]() ,求图2中的直线
,求图2中的直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目: 来源: 题型:
【题目】在抗击新冠肺炎的疫情中,某医院从3位女医生,5位男医生中选出4人参加援鄂医疗队,至少有一位女医生入选,其中女医生甲和男医生乙不能同时参加,则不同的选法共有种______(用数字填写答案).
查看答案和解析>>
科目: 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为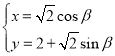 (
(![]() 为参数),直线
为参数),直线![]() 过原点且倾斜角为
过原点且倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)若相交于不同的两点![]() ,求
,求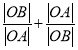 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com