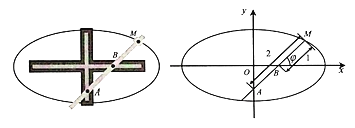
（1）将以射线Bx为始边，射线BM为终边的角xBM记为φ（0≤φ＜2π），用表示点M的坐标，并求出C的普通方程；

（2）已知过C的左焦点F，且倾斜角为α（0≤α）的直线l1与C交于D，E两点，过点F且垂直于l1的直线l2与C交于G，H两点.当，|GH|，依次成等差数列时，求直线l2的普通方程.

（1）|a|+|b+c﹣1|；

（2）（a3+b3+c3）（）≥3.

A.B.C.D.

A.B.C.D.

A.2B.4C.6D.8

【题目】已知双曲线C：1（a＞0，b＞0）的焦点分别为F1（﹣5，0），F2（5，0），P为C上一点，PF1⊥PF2，tan∠PF1F2，则C的方程为（ ）

A.x21B.y2＝1

C.1D.1

【题目】在直角坐标系中，曲线的参数方程为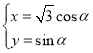（为参数），以坐标原点为极点，以轴的正半轴为极轴，建立极坐标系，点的极坐标，直线经过点，且倾斜角为.

（1）写出曲线的直角坐标方程和直线的标准参数方程；

（2）直线与曲线交于两点，直线的参数方程为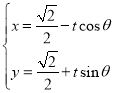（t为参数），直线与曲线交于两点，求证:.

【题目】学生考试中答对但得不了满分的原因多为答题不规范，具体表现为:解题结果正确，无明显推理错误，但语言不规范、缺少必要文字说明、卷面字迹不清、得分要点缺失等，记此类解答为“类解答”为评估此类解答导致的失分情况，某市教研室做了项试验:从某次考试的数学试卷中随机抽取若干属于“类解答”的题目，扫描后由近百名数学老师集体评阅，统计发现，满分12分的题，阅卷老师所评分数及各分数所占比例大约如下表:

某次数学考试试卷评阅采用“双评+仲裁”的方式，规则如下:两名老师独立评分，称为一评和二评，当两者所评分数之差的绝对值小于等于1分时，取两者平均分为该题得分；当两者所评分数之差的绝对值大于1分时，再由第三位老师评分，称之为仲裁，取仲裁分数和一、二评中与之接近的分数的平均分为该题得分；当一、二评分数和仲裁分数差值的绝对值相同时，取仲裁分数和前两评中较高的分数的平均分为该题得分.(假设本次考试阅卷老师对满分为12分的题目中的“类解答”所评分数及比例均如上表所示，比例视为概率，且一、二评与仲裁三位老师评分互不影响).

（1）本次数学考试中甲同学某题(满分12分)的解答属于“类解答”，求甲同学此题得分的分布列及数学期望;

（2）本次数学考试有6个解答题，每题满分12分，同学乙6个题的解答均为“类解答”.

①记乙同学6个题得分为的题目个数为计算事件的概率.

②同学丙的前四题均为满分，第5题为“类解答”，第6题得8分.以乙、丙两位同学解答题总分均值为依据，谈谈你对“类解答”的认识.

【题目】设.

（1）讨论在上的单调性；

（2）令，试证明在上有且仅有三个零点.

【题目】已知为坐标原点，为坐标平面内动点，且成等差数列.

（1）求动点的轨迹方程；

（2）设点的轨迹为曲线，过点作直线交于两点(不与原点重合)，是否存在轴上一定点，使得_________.若存在，求出定点，若不存在，说明理由.从“①作点关于轴的对称点，则三点共线；②”这两个条件中选一个，补充在上面的问题中并作答(注:如果选择两个条件分别作答，按第一个解答计分)