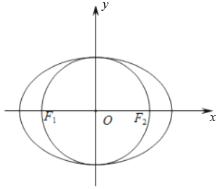
【题目】在平面直角坐标系xOy中，椭圆左、右焦点分别为，，离心率为，两准线间距离为8，圆O的直径为，直线l与圆O相切于第四象限点T，与y轴交于M点，与椭圆C交于点N（N点在T点上方），且．

（1）求椭圆C的标准方程；

（2）求直线l的方程；

（3）求直线l上满足到，距离之和为的所有点的坐标．

【题目】镇江市长江路江边春江潮广场要设计一尊鼎型塑像（如图1），塑像总高度为12米，塑像由两部分组成，上半部分由四根垂直于水平地面的等高垂直立柱组成（立柱上凸起部分忽略不计），下半部分由正四棱台的上底面四根水平横柱和正四棱台的四根侧棱斜柱组成，如图2所示．设计要求正棱台的水平横柱长度为4米，下底面边长为8米，设斜柱与地面的所成的角为．

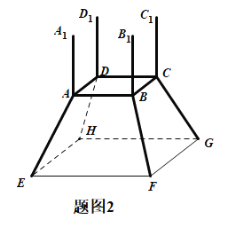
（1）用表示塑像上半部分立柱的高度，并求的取值范围？

（2）若该塑像上半部分立柱的造价为千元/米（立柱上凸起部分忽略不计），下半部分横柱和斜柱的造价都为2千元/米，问当为何值时，塑像总造价最低？

【题目】各项为正数的数列如果满足：存在实数，对任意正整数n，恒成立，且存在正整数n，使得或成立，则称数列为“紧密数列”，k称为“紧密数列”的“紧密度”．已知数列的各项为正数，前n项和为，且对任意正整数n，（A，B，C为常数）恒成立．

（1）当，，时，

①求数列的通项公式；

②证明数列是“紧密度”为3的“紧密数列”；

（2）当时，已知数列和数列都为“紧密数列”，“紧密度”分别为，，且，，求实数B的取值范围．

【题目】已知函数，其中是自然对数的底数．

（1）当时，求曲线在处的切线方程；

（2）如果对任意，不等式恒成立，求实数的取值范围；

（3）讨论函数的零点个数．

【题目】在平面直角坐标系中，以原点为极点，轴非负半轴为极轴，长度单位相同，建立极坐标系，曲线的极坐标方程为，直线过点，倾斜角为.

（1）将曲线的极坐标方程化为直角坐标方程，写出直线的参数方程的标准形式；

（2）已知直线交曲线于两点，求.

【题目】已知函数.

（1）若函数在定义域上的最大值为1，求实数的值；

（2）设函数，当时，对任意的恒成立，求满足条件的实数的最小整数值.

【题目】已知，是椭圆：的左、右焦点，离心率为，，是平面内两点，满足，线段的中点在椭圆上，周长为12．

（1）求椭圆的方程；

（2）若过的直线与椭圆交于，，求（其中为坐标原点）的取值范围．

【题目】某公司为了对某种商品进行合理定价，需了解该商品的月销售量（单位：万件）与月销售单价（单位：元/件）之间的关系，对近个月的月销售量和月销售单价数据进行了统计分析，得到一组检测数据如表所示：

（1）若用线性回归模型拟合与之间的关系，现有甲、乙、丙三位实习员工求得回归直线方程分别为：，和，其中有且仅有一位实习员工的计算结果是正确的．请结合统计学的相关知识，判断哪位实习员工的计算结果是正确的，并说明理由；

（2）若用模型拟合与之间的关系，可得回归方程为，经计算该模型和（1）中正确的线性回归模型的相关指数分别为和，请用说明哪个回归模型的拟合效果更好；

（3）已知该商品的月销售额为（单位：万元），利用（2）中的结果回答问题：当月销售单价为何值时，商品的月销售额预报值最大？（精确到）

参考数据：.

【题目】在中，设内角，，的对边分别为，，，且.

（1）若，，成等比数列，求证：；

（2）若（为锐角），.求中边上的高.

【题目】如图，在直三棱柱ABC－A1B1C1中，AA1ABAC2，AB⊥AC，M是棱BC的中点点P在线段A1B上．

（1）若P是线段A1B的中点，求直线MP与直线AC所成角的大小；

（2）若是的中点，直线与平面所成角的正弦值为，求线段BP的长度．