【题目】在平面直角坐标系xOy中，曲线C的参数方程为（为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为.

（1）求曲线C的极坐标方程和直线l的直角坐标方程；

（2）若射线与曲线C交于点A（不同于极点O），与直线l交于点B，求的最大值.

【题目】已知

（1）若a=1，且f(x)≥m在(0，+∞)恒成立，求实数m的取值范围；

（2）当时，若x=0不是f(x)的极值点，求实数a的取值.

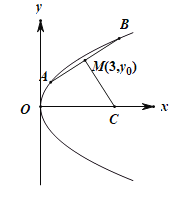
【题目】已知抛物线（）上的两个动点和，焦点为F.线段AB的中点为，且A，B两点到抛物线的焦点F的距离之和为8.

（1）求抛物线的标准方程；

（2）若线段AB的垂直平分线与x轴交于点C，求面积的最大值.

【题目】如图，几何体是圆柱的一部分，它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的，G是的中点.

(1)设P是上的一点，且AP⊥BE，求∠CBP的大小；

(2)当AB＝3，AD＝2时，求二面角E－AG－C的大小.

【题目】某校的一个社会实践调查小组，在对该校学生的良好“用眼习惯”的调查中，随机发放了120分问卷.对收回的100份有效问卷进行统计，得到如下列联表：

（1）现按女生是否能做到科学用眼进行分层，从45份女生问卷中抽取了6份问卷，从这6份问卷中再随机抽取3份，并记其中能做到科学用眼的问卷的份数，试求随机变量的分布列和数学期望；

（2）若在犯错误的概率不超过的前提下认为良好“用眼习惯”与性别有关，那么根据临界值表，最精确的的值应为多少？请说明理由.

附：独立性检验统计量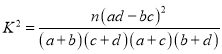，其中.

独立性检验临界值表：

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数

B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果，但防控要求不能降低

C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天

D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人

【题目】在平面直角坐标系xOy中，曲线C的参数方程为（为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为.

（1）求曲线C的极坐标方程和直线l的直角坐标方程；

（2）若射线与曲线C交于点A（不同于极点O），与直线l交于点B，求的最大值.

【题目】已知

（1）若a=1，且f(x)≥m在(0，+∞)恒成立，求实数m的取值范围；

（2）当时，若x=0不是f(x)的极值点，求实数a的取值.

【题目】已知抛物线（）上的两个动点和，焦点为F.线段AB的中点为，且A，B两点到抛物线的焦点F的距离之和为8.

（1）求抛物线的标准方程；

（2）若线段AB的垂直平分线与x轴交于点C，求面积的最大值.

将烦率视为概率

（1）试求消费者粽子购买量不低于300克的概率；

（2）若该市有100万名消费者，请估计该市今年在端午节期间应准备多少千克棕子才能满足市场需求（以各区间中点值作为该区间的购买量）.