
科目: 来源: 题型:
【题目】某航运公司用300万元买回客船一艘,此船投入营运后,毎月需开支燃油费、维修费、员工工资,已知每月燃油费7000元,第![]() 个月的维修费和工资支出为
个月的维修费和工资支出为![]() 元.
元.
(1)设月平均消耗为![]() 元,求
元,求![]() 与
与![]() (月)的函数关系;
(月)的函数关系;
(2)投入营运第几个月,成本最低?(月平均消耗最小)
(3)若第一年纯收入50万元(已扣除消耗),以后每年纯收入以5%递减,则多少年后可收回成本?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() (
(![]() 是常数,且
是常数,且![]() ),
),![]()
![]() ,数列
,数列![]() 的首项
的首项![]() ,
,![]()
![]() .
.
(1)证明:![]() 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() 是等比数列,求实数
是等比数列,求实数![]() 的值;
的值;
(3)当![]() 时,求数列
时,求数列![]() 的最小项.
的最小项.
查看答案和解析>>
科目: 来源: 题型:
【题目】在1与2之间插入![]() 个正数
个正数![]() ,使这
,使这![]() 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入![]() 个正数
个正数![]() ,使这
,使这![]() 个数成等差数列.记
个数成等差数列.记![]() .
.
(1)求数列![]() 和
和![]() 的通项;
的通项;
(2)当![]() 时,比较
时,比较![]() 与
与![]() 大小并证明结论.
大小并证明结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以![]() ,
,![]() 为顶点作正三角形
为顶点作正三角形![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正三角形
为顶点作正三角形![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正三角形
为顶点作正三角形![]() ,
,![]() ,如此继续下去.有如下结论:
,如此继续下去.有如下结论:

①所作的正三角形的边长构成公比为![]() 的等比数列;
的等比数列;
②每一个正三角形都有一个顶点在直线![]() 上;
上;
③第六个正三角形的不在第五个正三角形边上的顶点![]() 的坐标是
的坐标是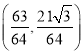 ;
;
④第![]() 个正三角形的不在第
个正三角形的不在第![]() 个正三角形边上的顶点
个正三角形边上的顶点![]() 的横坐标是
的横坐标是![]() ,则
,则![]() .
.
其中正确结论的序号是___________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目: 来源: 题型:
【题目】在数列![]() 中,
中,![]() ,若
,若![]() (
(![]() 为常数),则称
为常数),则称![]() 为“等差比数列”.下列是对“等差比数列”的判断:
为“等差比数列”.下列是对“等差比数列”的判断:
①![]() 不可能为
不可能为![]() ;②等差数列一定是等差比数列;
;②等差数列一定是等差比数列;
③等比数列一定是等差比数列;④等差比数列中可以有无数项为![]() .
.
其中正确的判断是( ).
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目: 来源: 题型:
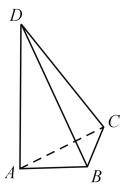
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2. 若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】
(注意:在试题卷上作答无效)
已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病动物为止;
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
求依方案甲所需化验次数不少于依方案乙所需化验次数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com