
科目: 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】己知圆![]() ,圆
,圆![]() .
.
(1)证明:圆![]() 与圆
与圆![]() 有公共点,并求公共点的轨迹
有公共点,并求公共点的轨迹![]() 的方程;
的方程;
(2)已知点![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与(1)中轨迹
的直线与(1)中轨迹![]() 相交于
相交于![]() 两点,记直线
两点,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)估计该天食堂利润不少于760元的概率;
(2)在直方图的需求量分组中,以区间中间值作为该区间的需求量,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题14分)在平面直角坐标系中,曲线C1的参数方程为![]() (a>b>0,
(a>b>0,![]() 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点![]() 对应的参数
对应的参数![]() .
.![]() 与曲线C2交于点
与曲线C2交于点![]() .
.
(1)求曲线C1,C2的直角坐标方程;
(2)![]() ,
,![]() 是曲线C1上的两点,求
是曲线C1上的两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】
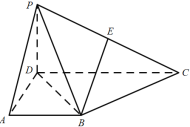
在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 中点,底面
中点,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() =90°,
=90°,![]() ,
,![]() .
.
(I)求证:![]()
![]() 平面
平面![]() ;
;
(II)求证:![]() 平面
平面![]() ;
;
(III)设![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 为45°.
为45°.
查看答案和解析>>
科目: 来源: 题型:
【题目】第24届冬季奥林匹克运动会将于2022年在北京-张家口举行,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高变成如右所示的茎叶图(单位: ![]() ):若身高在
):若身高在![]() 以上(包括
以上(包括![]() )定义为“高个子”,身高在
)定义为“高个子”,身高在![]() 以下(不包括
以下(不包括![]() )定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
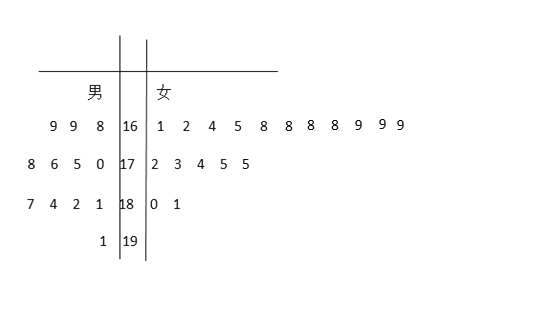
(1)如果分层抽样的方法从“高个子”和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用![]() 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为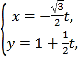 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】焦点在x轴上的椭圆C:![]() 经过点
经过点![]() ,椭圆C的离心率为
,椭圆C的离心率为![]() .
.![]() ,
,![]() 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.
(1)求椭圆的标准方程;
(2)若点M为![]() 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数![]() ,使得
,使得![]() ;若存在,请求出
;若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为![]() ,
,![]() ,……
,……![]() .
.
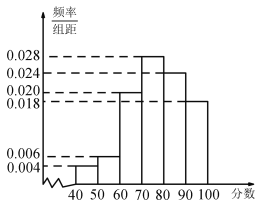
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在![]() 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com