
科目: 来源: 题型:
【题目】为了提高生产效益,某企业引进了一批新的生产设备,为了解设备生产产品的质量情况,分别从新、旧设备所生产的产品中,各随机抽取100件产品进行质量检测,所有产品质量指标值均在![]() 以内,规定质量指标值大于30的产品为优质品,质量指标值在
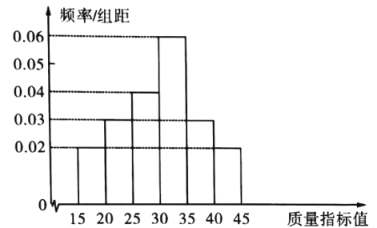
以内,规定质量指标值大于30的产品为优质品,质量指标值在![]() 的产品为合格品,旧设备所生产的产品质量指标值如频率分布直方图所示,新设备所生产的产品质量指标值如频数分布表所示.
的产品为合格品,旧设备所生产的产品质量指标值如频率分布直方图所示,新设备所生产的产品质量指标值如频数分布表所示.
质量指标值 | 频数 |
| 2 |
| 8 |
| 20 |
| 30 |
| 25 |
| 15 |
合计 | 100 |
(1)请分别估计新、旧设备所生产的产品的优质品率.
(2)优质品率是衡量一台设备性能高低的重要指标,优质品率越高说明设备的性能越高,根据已知图表数据填写下面列联表(单位:件),并判断是否有![]() 的把握认为“产品质量高于新设备有关”.
的把握认为“产品质量高于新设备有关”.
非优质品 | 优质品 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
附:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
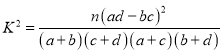 ,其中
,其中![]() .
.
(3)已知每件产品的纯利润y(单位:元)与产品质量指标值t的关系式为![]() 若每台新设备每天可以生产1000件产品,买一台新设备需要80万元,请估计至少需要生产多少天方可以收回设备成本.
若每台新设备每天可以生产1000件产品,买一台新设备需要80万元,请估计至少需要生产多少天方可以收回设备成本.
查看答案和解析>>
科目: 来源: 题型:
【题目】把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再把所得的函数图象上所有点的横坐标缩短到原来的
个单位长度,再把所得的函数图象上所有点的横坐标缩短到原来的![]() (纵坐标不变)得到函数
(纵坐标不变)得到函数![]() 的图象,关于
的图象,关于![]() 的说法有:①函数
的说法有:①函数![]() 的图象关于点
的图象关于点![]() 对称;②函数
对称;②函数![]() 的图象的一条对称轴是
的图象的一条对称轴是![]() ;③函数
;③函数![]() 在
在![]() 上的最上的最小值为
上的最上的最小值为![]() ;④函数
;④函数![]() 上单调递增,则以上说法正确的个数是( )
上单调递增,则以上说法正确的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目: 来源: 题型:
【题目】《周髀算经》是我国古老的天文学和数学著作,其书中记载:一年有二十四个节气,每个节气晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测影子的长度),夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降是连续的九个节气,其晷长依次成等差数列,经记录测算,这九个节气的所有晷长之和为49.5尺,夏至、大暑、处暑三个节气晷长之和为10.5尺,则立秋的晷长为( )
A.1.5尺B.2.5尺C.3.5尺D.4.5尺
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,以
时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)与![]() 平行的直线
平行的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,若平行线
两点,若平行线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,且
,且![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍(O为坐标原点),求
倍(O为坐标原点),求![]() 和
和![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】网购已成为当今消费者喜欢的购物方式.某机构对A、B、C、D四家同类运动服装网店的关注人数 x(千人)与其商品销售件数 y(百件)进行统计对比,得到如下表格:

由散点图知,可以用回归直线 来近似刻画它们之间的关系.
参考公式: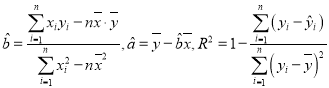
(1)求 y与 x的回归直线方程;
(2)在(1)的回归模型中,请用![]() 说明销售件数的差异有多大程度是由关注人数引起的?(精确到
说明销售件数的差异有多大程度是由关注人数引起的?(精确到![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 和点D(2,0),直线
和点D(2,0),直线 ![]() 与抛物线C交于不同两点A、B,直线BD与抛物线C交于另一点E.给出以下判断:
与抛物线C交于不同两点A、B,直线BD与抛物线C交于另一点E.给出以下判断:
①直线OB与直线OE的斜率乘积为-2; ②![]() 轴; ③以BE为直径的圆与抛物线准线相切;
轴; ③以BE为直径的圆与抛物线准线相切;
其中,所有正确判断的序号是( )
A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥中![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]()
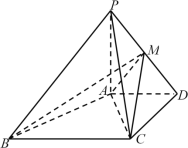
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,如果存在,求
,如果存在,求![]() 与平面
与平面![]() 所成的角的正弦值,如果不存在,请说明理由.
所成的角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com