【题目】已知离心率为的椭圆的左顶点为，左焦点为，及点，且、、成等比数列．

（1）求椭圆的方程；

（2）斜率不为的动直线过点且与椭圆相交于、两点，记，线段上的点满足，试求（为坐标原点）面积的取值范围．

【题目】千百年来，我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化，总结了丰富的“看云识天气”的经验，并将这些经验编成谚语，如“天上钩钩云，地上雨淋淋”“日落云里走，雨在半夜后”……小波同学为了验证“日落云里走，雨在半夜后”，观察了所在地区的天日落和夜晚天气，得到如下列联表：

参考公式：.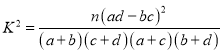

临界值表：

（1）根据上面的列联表判断能否有的把握认为“当晚下雨”与“‘日落云里走’出现”有关？

（2）小波同学为进一步认识其规律，对相关数据进行分析，现从上述调查的“夜晚未下雨”天气中按分层抽样法抽取天，再从这天中随机抽出天进行数据分析，求抽到的这天中仅有天出现“日落云里走”的概率．

（1）求不等式f（x）≥8的解集；

（2）若a＞0，b＞0，且函数F（x）＝f（x）﹣3a﹣2b有唯一零点x0，证明：f（x0）．

【题目】在平面直角坐标系xOy中，已知曲线C的参数方程为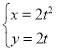（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρ（cosθ+sinθ）＝8．

（1）求曲线C和直线l的直角坐标方程；

（2）若射线m的极坐标方程为θ（ρ≥0），设m与C相交于点M（非坐标原点），m与l相交于点N，点P（6，0），求△PMN的面积．

【题目】已知函数f(x)（a＞0）．

（1）证明：当x∈[1，+∞）时，f(x)≥1．

（2）当0<a≤1时，对于任意的x∈(0，+∞)，f(x)≥m，求整数m的最大值．

【题目】已知椭圆C：1（a＞b＞0）的右焦点为F，离心率为，且有3a2＝4b2+1．

（1）求椭圆C的标准方程；

（2）过点F的直线l与椭圆C交于M，N两点，过点M作直线x＝3的垂线，垂足为点P，证明直线NP经过定点，并求出这个定点的坐标．

【题目】在四棱锥P﹣ABCD中，底面四边形ABCD是一个菱形，且∠ABC，AB＝2，PA⊥平面ABCD．

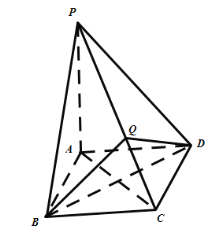
（1）若Q是线段PC上的任意一点，证明：平面PAC⊥平面QBD．

（2）当平面PBC与平面PDC所成的锐二面角的余弦值为时，求PA的长．

（1）若采用分层抽样抽取10人，分别求高一、高二、高三应抽取的人数．

（2）若被抽取的10人中，有6人每天学时超过7小时，有4人每天学时不足4小时，现从这10人中，再随机抽取4人做进一步调查．

（i）记事件A为“被抽取的4人中至多有1人学时不足4小时”，求事件A发生的概率；

（ii）用ξ表示被抽取的4人中学时不足4小时的人数，求随机变量ξ的分布列和数学期望．

【题目】△ABC的内角A，B，C的对边分别为a，b，c，且asinBbcosA+a＝bcosC+ccosB．

（1）求A；

（2）若a，点D在BC上，且AD⊥AC，当△ABC的周长取得最大值时，求BD的长．

【题目】已知F1（﹣c，0），F2（c，0）分别为双曲线C：1（a＞0，b＞0）的左、右焦点，直线l：1与C交于M，N两点，线段MN的垂直平分线与x轴交于T（﹣5c，0），则C的离心率为（ ）

A.B.C.D.