
【题目】已知函数f(x)![]() (a>0).
(a>0).
(1)证明:当x∈[1,+∞)时,f(x)≥1.
(2)当0<a≤1时,对于任意的x∈(0,+∞),f(x)≥m,求整数m的最大值.
【答案】(1)见解析(2)m的最大整数值为0.
【解析】
(1)求导可知f′(x)>0,则f(x)在[1,+∞)上是增函数,进而得证;
(2)依题意,当0<x<1时,![]() ,令
,令![]() ,则问题转化为g(x)≥m在(0,1)上恒成立,利用导数求出函数g(x)的最小值即可.
,则问题转化为g(x)≥m在(0,1)上恒成立,利用导数求出函数g(x)的最小值即可.
(1)证明:![]() ,
,
∵a>0,x≥1,
∴f′(x)>0,f(x)在[1,+∞)上是增函数,
∴f(x)≥ f(1)=1;
(2)当x≥1时,由(1)知f(x)≥1,故m≤1;
当0<x<1时,因为0<a≤1,所以![]() ,
,
令![]() ,故问题转化为g(x)≥m在(0,1)上恒成立,
,故问题转化为g(x)≥m在(0,1)上恒成立,![]() ,
,
令h(x)=x+1+lnx,易知h(x)在(0,1)上单调递增,
∵h(e﹣2)<0,h(1)>0,
∴存在![]() ,使得h(x0)=x0+1+lnx0=0,
,使得h(x0)=x0+1+lnx0=0,
当x∈(0,x0)时,g′(x)< 0,当x∈(x0,1)时,g′(x)>0,
∴g(x)在x=x0处取得最小值,![]() ,
,
由于x0+1+lnx0=0,于是![]() ,
,
∵![]() ,
,
∴0<g(x0)<1,
综上所述,m的最大整数值为0.


科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则
①OE⊥BD1;
②OE![]() 面A1C1D;
面A1C1D;
③三棱锥A1﹣BDE的体积不是定值;
④OE与A1C1所成的最大角为90°.
上述命题中正确的个数是( )
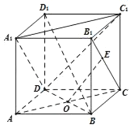
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
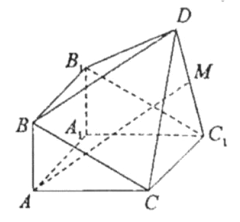
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1(﹣c,0),F2(c,0)分别为双曲线C:![]() 1(a>0,b>0)的左、右焦点,直线l:
1(a>0,b>0)的左、右焦点,直线l:![]() 1与C交于M,N两点,线段MN的垂直平分线与x轴交于T(﹣5c,0),则C的离心率为( )
1与C交于M,N两点,线段MN的垂直平分线与x轴交于T(﹣5c,0),则C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 、
、![]() 两点分别是椭圆
两点分别是椭圆![]() 的上、下顶点,
的上、下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 、
、![]() 的动点,直线
的动点,直线![]() 、
、![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 、
、![]() 两点,点
两点,点![]() ,试问:
,试问:![]() 外接圆是否恒过
外接圆是否恒过![]() 轴上的定点(异于点
轴上的定点(异于点![]() )?若是,求该定点坐标;若否,说明理由.
)?若是,求该定点坐标;若否,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(Ⅱ)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
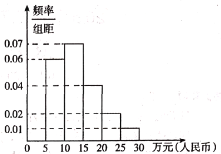
以(Ⅰ)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: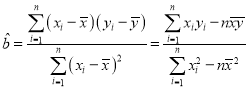 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com