
科目: 来源: 题型:
【题目】如图,已知抛物线![]() ,设直线
,设直线![]() 经过点
经过点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 两点,抛物线
两点,抛物线![]() 在
在![]() 、
、![]() 两点处的切线相交于点
两点处的切线相交于点![]() ,直线
,直线![]() ,
,![]() 分别与
分别与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.

(1)求点![]() 的轨迹方程
的轨迹方程
(2)当点![]() 不在
不在![]() 轴上时,记
轴上时,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
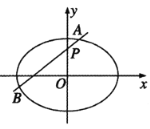
【题目】已知椭圆![]() 的离心率e满足
的离心率e满足![]() ,以坐标原点为圆心,椭圆C的长轴长为半径的圆与直线
,以坐标原点为圆心,椭圆C的长轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆C的方程;
(2)过点P(0,1)的动直线![]() (直线
(直线![]() 的斜率存在)与椭圆C相交于A,B两点,问在y轴上是否存在与点P不同的定点Q,使得
的斜率存在)与椭圆C相交于A,B两点,问在y轴上是否存在与点P不同的定点Q,使得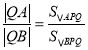 恒成立?若存在,求出定点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出定点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某人玩掷正方体骰子走跳棋的游戏,已知骰子每面朝上的概率都是![]() ,棋盘上标有第0站,第1站,第2站,……,第100站.一枚棋子开始在第0站,选手每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,棋子向前跳两站;若掷出其余点数,则棋子向前跳一站,直到跳到第99站或第100站时,游戏结束;设游戏过程中棋子出现在第
,棋盘上标有第0站,第1站,第2站,……,第100站.一枚棋子开始在第0站,选手每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,棋子向前跳两站;若掷出其余点数,则棋子向前跳一站,直到跳到第99站或第100站时,游戏结束;设游戏过程中棋子出现在第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀骰子3次后,求棋子所走站数之和X的分布列与数学期望;
(2)证明:![]() ;
;
(3)若最终棋子落在第99站,则记选手落败,若最终棋子落在第100站,则记选手获胜,请分析这个游戏是否公平.
查看答案和解析>>
科目: 来源: 题型:
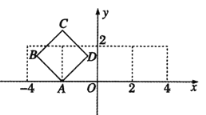
【题目】在平面直角坐标系![]() 中,如图放置的边长为2的正方形ABCD沿
中,如图放置的边长为2的正方形ABCD沿![]() 轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点
轴滚动(无滑动滚动),点D恰好经过坐标原点,设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 的判断正确的是( )
的判断正确的是( )
A.函数![]() 在
在![]() 上有两个零点
上有两个零点
B.函数![]() 是偶函数
是偶函数
C.函数![]() 在
在![]() 上单调递增
上单调递增
D.对任意的![]() ,都有
,都有![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】“杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广,发明了“三系法”籼型杂交水稻,成功研究出“两系法”杂交水稻,创建了超级杂交稻技术体系,为我国粮食安全、农业科学发展和世界粮食供给做出了杰出贡献;某杂交水稻种植研究所调查某地水稻的株高,得出株高(单位:cm)服从正态分布,其密度曲线函数为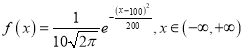 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.该地水稻的平均株高为100cm
B.该地水稻株高的方差为10
C.随机测量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大
D.随机测量一株水稻,其株高在(80,90)和在(100,110)(单位:cm)的概率一样大
查看答案和解析>>
科目: 来源: 题型:
【题目】在脱贫攻坚中,某市教育局定点帮扶前进村![]() 户贫困户.驻村工作队对这
户贫困户.驻村工作队对这![]() 户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限
户村民的贫困程度以及家庭平均受教育程度进行了调査,并将该村贫困户按贫困程度分为“绝对贫困户”与“相对贫困户”,同时按家庭平均受教育程度分为“家庭平均受教育年限![]() 年”与“家庭平均受教育年限
年”与“家庭平均受教育年限![]() 年”,具体调査结果如下表所示:
年”,具体调査结果如下表所示:
平均受教育年限 | 平均受教育年限 | 总计 | |
绝对贫困户 | 10 | 40 | 50 |
相对贫困户 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
(1)为了参加扶贫办公室举办的贫困户“谈心谈话”活动,现通过分层抽样从“家庭平均受教育年限![]() 年”的
年”的![]() 户贫困户中任意抽取
户贫困户中任意抽取![]() 户,再从所抽取的
户,再从所抽取的![]() 户中随机抽取
户中随机抽取![]() 户参加“谈心谈话”活动,求至少有
户参加“谈心谈话”活动,求至少有![]() 户是绝对贫困户的概率;
户是绝对贫困户的概率;
(2)根据上述表格判断:是否有![]() 的把握认为贫困程度与家庭平均受教育程度有关?
的把握认为贫困程度与家庭平均受教育程度有关?
参考公式:![]()
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
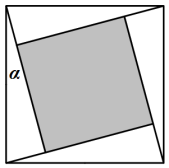
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明![]() 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形
如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形![]() 若直角三角形中较小的锐角
若直角三角形中较小的锐角![]() ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com