
科目: 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为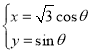 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换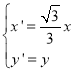 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴,建立极坐标系.设
轴的正半轴为极轴,建立极坐标系.设![]() 点的极坐标为
点的极坐标为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:已知正方形![]() 的边长为
的边长为![]() ,沿着对角线
,沿着对角线![]() 将
将![]() 折起,使
折起,使![]() 到达
到达![]() 的位置,且
的位置,且![]() .
.
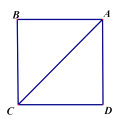
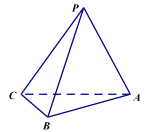
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且满足直线
上,且满足直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】正方体![]() 的棱长为2,动点
的棱长为2,动点![]() 在对角线
在对角线![]() 上,过点
上,过点![]() 作垂直于
作垂直于![]() 的平面
的平面![]() ,记平面
,记平面![]() 截正方体得到的截面多边形(含三角形)的周长为
截正方体得到的截面多边形(含三角形)的周长为![]() ,设
,设![]() .
.
(1)下列说法中,正确的编号为__________.
①截面多边形可能为四边形;②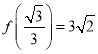 ;③函数
;③函数![]() 的图象关于
的图象关于![]() 对称.
对称.
(2)当![]() 时,三棱锥
时,三棱锥![]() 的外接球的表面积为__________.
的外接球的表面积为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年11月18日国际射联步手枪世界杯总决赛在莆田市综合体育馆开幕,这是国际射联步手枪世界杯总决赛时隔10年再度走进中国.为了增强趣味性,并实时播报现场赛况,我校现场小记者李明和播报小记者王华设计了一套播报转码法,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的![]() 的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式:
的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式: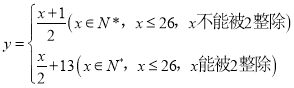 ,将明文转换成密文,如
,将明文转换成密文,如![]() ,即
,即![]() 变换成
变换成![]() ,即
,即![]() 变换成
变换成![]() .若按上述规定,若王华收到的密文是
.若按上述规定,若王华收到的密文是![]() ,那么原来的明文是( )
,那么原来的明文是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换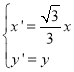 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴,建立极坐标系.设
轴的正半轴为极轴,建立极坐标系.设![]() 点的极坐标为
点的极坐标为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年11月18日国际射联步手枪世界杯总决赛在莆田市综合体育馆开幕,这是国际射联步手枪世界杯总决赛时隔10年再度走进中国.为了增强趣味性,并实时播报现场赛况,我校现场小记者李明和播报小记者王华设计了一套播报转码法,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的![]() 的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式:
的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式: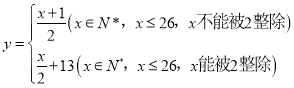 ,将明文转换成密文,如
,将明文转换成密文,如![]() ,即
,即![]() 变换成
变换成![]() ,即
,即![]() 变换成
变换成![]() .若按上述规定,若王华收到的密文是
.若按上述规定,若王华收到的密文是![]() ,那么原来的明文是( )
,那么原来的明文是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设集合![]() 由满足下列两个条件的数列
由满足下列两个条件的数列![]() 构成:①
构成:①![]() ②存在实数
②存在实数![]() 使
使![]() 对任意正整数
对任意正整数![]() 都成立.
都成立.
(1)现在给出只有5项的有限数列![]() 其中
其中![]() ;
;![]() 试判断数列
试判断数列![]() 是否为集合
是否为集合![]() 的元素;
的元素;
(2)数列![]() 的前
的前![]() 项和为
项和为![]() 且对任意正整数
且对任意正整数![]() 点
点![]() 在直线
在直线![]() 上,证明:数列
上,证明:数列![]() 并写出实数
并写出实数![]() 的取值范围;
的取值范围;
(3)设数列![]() 且对满足条件②中的实数
且对满足条件②中的实数![]() 的最小值
的最小值![]() 都有
都有![]() 求证:数列
求证:数列![]() 一定是单调递增数列.
一定是单调递增数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆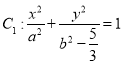 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在x轴,y轴上的截距分别为
在x轴,y轴上的截距分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 是椭圆
是椭圆![]() 上不同两点,
上不同两点,![]() 轴,圆E过
轴,圆E过![]() ,且椭圆
,且椭圆![]() 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆![]() 是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com