
科目: 来源: 题型:
【题目】
在平面直角坐标系中,以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为:![]() ,经过点
,经过点![]() ,倾斜角为
,倾斜角为![]() 的直线l与曲线C交于A,B两点
的直线l与曲线C交于A,B两点
(I)求曲线C的直角坐标方程和直线l的参数方程;
(Ⅱ)求![]() 的值。
的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]()
![]() 的左顶点为A,且椭圆E经过
的左顶点为A,且椭圆E经过![]() 与坐标轴不垂直的直线l与椭圆E交于C,D两点,且直线AC和直线AD的斜率之积为
与坐标轴不垂直的直线l与椭圆E交于C,D两点,且直线AC和直线AD的斜率之积为![]() .
.
(I)求椭圆E的标准方程;
(Ⅱ)求证:直线l过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】为弘扬中华民族优秀传统文化,树立正确的价值导向,落实立德树人根本任务,某市组织30000名高中学生进行古典诗词知识测试,根据男女学生人数比例,使用分层抽样的方法从中随机抽取100名学生,记录他们的分数,整理所得频率分布直方图如图:
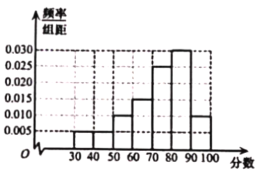
(Ⅰ)规定成绩不低于60分为及格,不低于85分为优秀,试估计此次测试的及格率及优秀率;
(Ⅱ)试估计此次测试学生成绩的中位数;
(Ⅲ)已知样本中有![]() 的男生分数不低于80分,且样本中分数不低于80分的男女生人数相等,试估计参加本次测试30000名高中生中男生和女生的人数.
的男生分数不低于80分,且样本中分数不低于80分的男女生人数相等,试估计参加本次测试30000名高中生中男生和女生的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志是“连续10日,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:总体平均数为3,中位数为4;
乙地:总体平均数为1,总体方差大于0;
丙地:总体平均数为2,总体方差为3;
丁地:中位数为2,众数为3;
则甲、乙、两、丁四地中,一定没有发生大规模群体感染的是( )
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目: 来源: 题型:
【题目】一件刚出土的珍贵文物要在博物馆大厅中央展出,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积0.5立方米,其底部是直径为0.9米的圆形,要求文物底部与玻璃罩底边至少间隔0.3米,文物顶部与玻璃罩上底面至少间隔0.2米,气体每立方米1000元,则气体费用最少为( )元

A.4500B.4000C.2880D.2380
查看答案和解析>>
科目: 来源: 题型:
【题目】“剑桥学派”创始人之一数学家哈代说过:“数学家的造型,同画家和诗人一样,也应当是美丽的”;古希腊数学家毕达哥拉斯创造的“黄金分割”给我们的生活处处带来美;我国古代数学家赵爽创造了优美“弦图”.“弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,则
,则![]() 等于( )
等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一个无理数列(即对任意的
为一个无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式;
的通项公式;
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为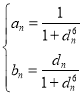 ;
;
(3)已知![]() ,
,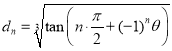 ,试计算
,试计算![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】一青蛙从点![]() 开始依次水平向右和竖直向上跳动,其落点坐标依次是
开始依次水平向右和竖直向上跳动,其落点坐标依次是![]() ,(如图,
,(如图,![]() 的坐标以已知条件为准),
的坐标以已知条件为准),![]() 表示青蛙从点
表示青蛙从点![]() 到点
到点![]() 所经过的路程.
所经过的路程.
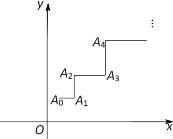
(1)点![]() 为抛物线
为抛物线![]()
![]() 准线上一点,点
准线上一点,点![]() ,
,![]() 均在该抛物线上,并且直线
均在该抛物线上,并且直线![]()
![]() 经过该抛物线的焦点,证明
经过该抛物线的焦点,证明![]() ;
;
(2)若点![]() 要么落在
要么落在![]() 所表示的曲线上,要么落在
所表示的曲线上,要么落在![]() 所表示的曲线上,并且
所表示的曲线上,并且![]() ,试写出
,试写出![]() (不需证明);
(不需证明);
(3)若点![]() 要么落在
要么落在![]() 所表示的曲线上,要么落在
所表示的曲线上,要么落在![]() 所表示的曲线上,并且
所表示的曲线上,并且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com