
科目: 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)的一种,现有十二生肖的吉物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学选取的礼物都满意,那么不同的选法有( )
A. 50种B. 60种C. 70种D. 90种
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为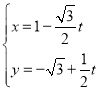 (t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系.曲线C的极坐标方程为
(t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系.曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)设点![]() ,直线l与曲线C相交于A,B两点,求
,直线l与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点,其中直线l不过原点.
两点,其中直线l不过原点.
(1)求椭圆C的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,其中
,其中![]() 且
且![]() .记
.记![]() 的面积为S.分别以
的面积为S.分别以![]() 为直径的圆的面积依次为
为直径的圆的面积依次为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中a为常数,e是自然对数的底数,
,其中a为常数,e是自然对数的底数,![]() ,曲线
,曲线![]() 在其与y轴的交点处的切线记作
在其与y轴的交点处的切线记作![]() ,曲线
,曲线![]() 在其与x轴的交点处的切线记作
在其与x轴的交点处的切线记作![]() ,且
,且![]() .
.
(1)求![]() 之间的距离;
之间的距离;
(2)对于函数![]() 和
和![]() 的公共定义域中的任意实数
的公共定义域中的任意实数![]() ,称
,称![]() 的值为函数
的值为函数![]() 和
和![]() 在
在![]() 处的偏差.求证:函数
处的偏差.求证:函数![]() 和
和![]() 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
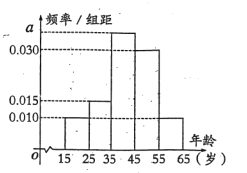
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,设第2组抽到![]() 人,求随机变量
人,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)在函数![]() 的图象上取
的图象上取![]() 两个不同的点,令直线AB的斜率
两个不同的点,令直线AB的斜率
为k,则在函数的图象上是否存在点![]() ,且
,且![]() ,使得
,使得![]() ?若存
?若存
在,求A,B两点的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过点
的焦距为2,过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆的右焦点为F,定点![]() ,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线
,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线![]() 的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com