
科目: 来源: 题型:
【题目】设数列![]() 的通项公式为
的通项公式为![]() (
(![]() ,
, ![]() ),数列
),数列![]() 定义如下:对于正整数
定义如下:对于正整数![]() ,
, ![]() 是使得不等式
是使得不等式![]() 成立的所有
成立的所有![]() 中的最小值.
中的最小值.
(1)若![]() ,
, ![]() ,求
,求![]() ;
;
(2)若![]() ,
, ![]() ,求数列
,求数列![]() 的前
的前![]() 项和公式;
项和公式;
(3)是否存在![]() 和
和![]() ,使得
,使得![]()
![]() ?如果存在,求
?如果存在,求![]() 和
和![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】将数列![]() 中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
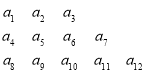
……
记表中的第一列数![]() ,
,![]() ,
,![]() ,…,构成数列
,…,构成数列![]() .
.
(1)设![]() ,求m的值;
,求m的值;
(2)若![]() ,对于任何
,对于任何![]() ,都有
,都有![]() ,且
,且![]() .求数列
.求数列![]() 的通项公式.
的通项公式.
(3)对于(2)中的数列![]() ,若上表中每一行的数按从左到右的顺序均构成公比为q(
,若上表中每一行的数按从左到右的顺序均构成公比为q(![]() )的等比数列,且
)的等比数列,且![]() ,求上表中第k(
,求上表中第k(![]() )行所有项的和
)行所有项的和![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】数列{2n﹣1}的前n项1,3,7,…,2n﹣1组成集合![]() (n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
(n∈N*),从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),记Sn=T1+T2+…+Tn,例如当n=1时,A1={1},T1=1,S1=1;当n=2时,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,试写出Sn=__.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,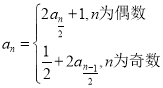 ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(3)对任意的![]() ,
,![]() ,在数列
,在数列![]() 中是否存在连续的
中是否存在连续的![]() 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这![]() 项,并证明这
项,并证明这![]() 项构成等差数列:若不存在,请说明理由.
项构成等差数列:若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,由半圆![]() 和部分抛物线
和部分抛物线![]() 合成的曲线
合成的曲线![]() 称为“羽毛球开线”,曲线
称为“羽毛球开线”,曲线![]() 与
与![]() 轴有
轴有![]() 两个焦点,且经过点
两个焦点,且经过点![]()

(1)求![]() 的值;
的值;
(2)设![]()
![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与“羽毛球形线”相交于点
与“羽毛球形线”相交于点![]() 三点,问是否存在实数
三点,问是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】经市场调查,某商品每吨的价格为![]() 万元时,该商品的月供给量为
万元时,该商品的月供给量为![]() 吨,
吨,![]() ;月需求量为
;月需求量为![]() 吨,
吨,![]() ,当该商品的需求量大于供给量时,销售量等于供给量;当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
,当该商品的需求量大于供给量时,销售量等于供给量;当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
(1)已知![]() ,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6万元,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 定义在实数集
定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() ,
,![]()
![]() 称为
称为![]() 的特征根.
的特征根.
(1)讨论函数的奇偶性,并说明理由;
(2)求![]() 表达式;
表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() 、最小值记作
、最小值记作![]() ,令
,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,若在区间
,若在区间![]() 内有且只有一个实数
内有且只有一个实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(1)判断函数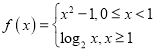 在区间
在区间![]() 内是否具有唯一零点,说明理由:
内是否具有唯一零点,说明理由:
(2)已知向量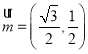 ,
,![]() ,
,![]() ,证明
,证明![]() 在区间
在区间![]() 内具有唯一零点.
内具有唯一零点.
(3)若函数![]() 在区间
在区间![]() 内具有唯一零点,求实数
内具有唯一零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com