
科目: 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2014年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为
![]() 元/件,假定厂家的生产能力完全能满足市场的销售需求.
元/件,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】设双曲线方程为![]() ,过其右焦点且斜率不为零的直线
,过其右焦点且斜率不为零的直线![]() 与双曲线交于A,B两点,直线
与双曲线交于A,B两点,直线![]() 的方程为
的方程为![]() ,A,B在直线
,A,B在直线![]() 上的射影分别为C,D.
上的射影分别为C,D.
(1)当![]() 垂直于x轴,
垂直于x轴,![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(2)![]() ,
,![]() 的斜率为正实数,A在第一象限,B在第四象限,试比较
的斜率为正实数,A在第一象限,B在第四象限,试比较![]() 与1的大小;
与1的大小;
(3)是否存在实数![]() ,使得对满足题意的任意
,使得对满足题意的任意![]() ,直线
,直线![]() 和直线
和直线![]() 的交点总在
的交点总在![]() 轴上,若存在,求出所有的
轴上,若存在,求出所有的![]() 值和此时直线
值和此时直线![]() 和
和![]() 交点的位置;若不存在,请说明理由.
交点的位置;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列![]() 满足
满足![]() ,其中A,B是两个确定的实数,
,其中A,B是两个确定的实数,![]()
(1)若![]() ,求
,求![]() 的前n项和;
的前n项和;
(2)证明:![]() 不是等比数列;
不是等比数列;
(3)若![]() ,数列
,数列![]() 中除去开始的两项外,是否还有相等的两项,并证明你的结论.
中除去开始的两项外,是否还有相等的两项,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如题所示:扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条三条商业街道PQ、QR、RP,要求街道PQ与AB垂直,街道PR与AC垂直,直线PQ表示第三条街道。
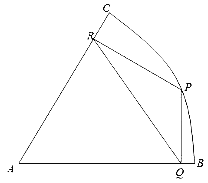
(1)如果P位于弧BC的中点,求三条街道的总长度;
(2)由于环境的原因,三条街道PQ、PR、QR每年能产生的经济效益分别为每千米300万元、200万元及400万元,问:这三条街道每年能产生的经济总效益最高为多少?(精确到1万元)
查看答案和解析>>
科目: 来源: 题型:
【题目】市场上有一种新型的强力洗衣粉,特点是去污速度快,已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中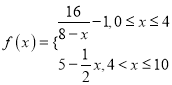 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
(1)若只投放一次4个单位的洗衣液,则有效去污时间可能达几分钟?
(2)若先投放2个单位的洗衣液,6分钟后投放![]() 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: ![]() 取
取![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
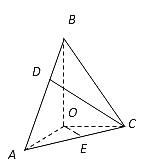
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
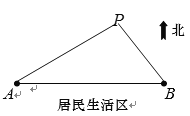
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为![]() .
.
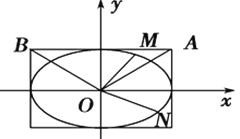
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)不过原点![]() 的直线与椭圆
的直线与椭圆![]() 交于两点
交于两点![]() 、
、![]() ,且直线
,且直线![]() 、
、![]() 、
、![]() 的斜率依次成等比数列,问:直线是否定向的,请说明理由.
的斜率依次成等比数列,问:直线是否定向的,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 是公差
是公差![]() 的等差数列,且
的等差数列,且![]() .
.
(1)求![]() 的前
的前![]() 项的和
项的和![]() ;
;
(2)若![]() ,问在数列
,问在数列![]() 中是否存在一项
中是否存在一项![]() (
(![]() 是正整数),使得
是正整数),使得![]() 成等比数列,若存在,求出
成等比数列,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若存在自然数![]() (
(![]() 是正整数),满足
是正整数),满足![]() ,使得
,使得![]() 成等比数列,求所有整数
成等比数列,求所有整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com