
科目: 来源: 题型:
【题目】在中老年人群体中,肠胃病是一种高发性疾病某医学小组为了解肠胃病与运动之间的联系,调查了50位中老年人每周运动的总时长(单位:小时),将数据分成[0,4),[4,8),[8,14),[14,16),[16,20),[20,24]6组进行统计,并绘制出如图所示的柱形图.
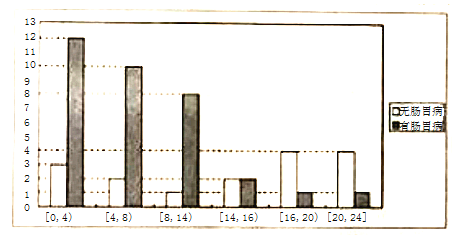
图中纵轴的数字表示对应区间的人数现规定:每周运动的总时长少于14小时为运动较少.
每周运动的总时长不少于14小时为运动较多.
(1)根据题意,完成下面的2×2列联表:
有肠胃病 | 无肠胃病 | 总计 | |
运动较多 | |||
运动较少 | |||
总计 |
(2)能否有99.9%的把握认为中老年人是否有肠胃病与运动有关?
附:K2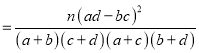 (n=a+b+c+d)
(n=a+b+c+d)
P(K2≥k) | 0.0.50 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.

(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量
的回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量![]() 约为多少?
约为多少?
附:相关系数公式
 ,参考数据:
,参考数据:![]() ,
,![]() .
.
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A.从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样
B.某地气象局预报:5月9日本地降水概率为![]() ,结果这天没下雨,这表明天气预报并不科学
,结果这天没下雨,这表明天气预报并不科学
C.在回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 增加0.1个单位
增加0.1个单位
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() 且椭圆上存在一点P,满足.
且椭圆上存在一点P,满足.![]() ,
,![]()
(1)求椭圆C的标准方程;
(2)已知A,B分别是椭圆C的左、右顶点,过![]() 的直线交椭圆C于M,N两点,记直线
的直线交椭圆C于M,N两点,记直线![]() ,
,![]() 的交点为T,是否存在一条定直线l,使点T恒在直线l上?
的交点为T,是否存在一条定直线l,使点T恒在直线l上?
查看答案和解析>>
科目: 来源: 题型:
【题目】为推行“高中新课程改革”,某数学老师分别用“传统教学”和“新课程”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果.期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于120分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 7 | 5 | 4 | 3 | 1 |
乙班频数 | 1 | 2 | 5 | 5 | 7 |
(1)从以上统计数据填写下面![]() 列联表,并判断能否犯错误的频率不超过0.01的前提下认为“成绩优良与教学方式有关”?
列联表,并判断能否犯错误的频率不超过0.01的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
P( | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: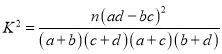 ,其中
,其中![]() .临界值表如上表:
.临界值表如上表:
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核,在这8人中,记成绩不优良的乙班人数为X,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com