
科目: 来源: 题型:
【题目】“绿水青山就是金山银山”的理念越来越深入人心,据此,某网站调查了人们对生态文明建设的关注情况,调查数据表明,参与调查的人员中关注生态文明建设的约占80%.现从参与调查的关注生态文明建设的人员中随机选出200人,并将这200人按年龄(单位:岁)分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65],得到的频率分布直方图如图所示.
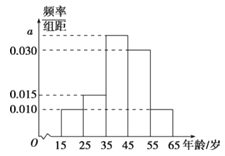
(Ⅰ)求这200人的平均年龄(每一组用该组区间的中点值作为代表)和年龄的中位数(保留一位小数);
(Ⅱ)现在要从年龄在第1,2组的人员中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求抽取的3人中恰有2人的年龄在第2组中的概率;
(Ⅲ)若从所有参与调查的人(人数很多)中任意选出3人,设这3人中关注生态文明建设的人数为X,求随机变量X的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为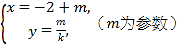 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目: 来源: 题型:
【题目】为缓解城市道路交通压力,促进城市道路交通有序运转,减少机动车尾气排放对空气质量的影响,西安市人民政府决定:自2019年3月18日至2020年3月13日在相关区域实施工作日机动车尾号限行交通管理措施.已知每辆机动车每周一到周五都要限行一天,周末(周六和周日)不限行.某公司有A,B,C,D,E五辆车,每天至少有四辆车可以上路行驶.已知E车周四限行,B车昨天限行,从今天算起,A,C 两辆车连续四天都能上路行驶,E车明天可以上路,由此可知下列推测一定正确的是( )
A.今天是周四B.今天是周六C.A车周三限行D.C车周五限行
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,过焦点且与
,过焦点且与![]() 轴垂直的直线被椭圆
轴垂直的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() ,
,![]() ,过点
,过点![]() 的任意一条直线
的任意一条直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是2019年11月1日到11月20日,某地区甲流疫情新增数据的走势图.
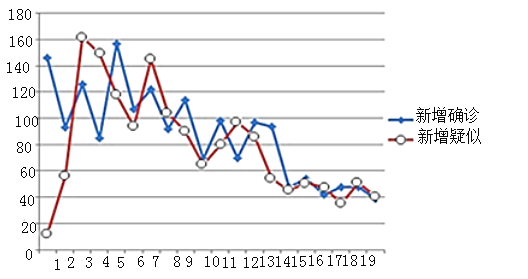
(1)从这20天中任选1天,求新增确诊和新增疑似的人数都超过100的概率;
(2)从新增确诊的人数超过100的日期中任选两天,用X表示新增确诊的人数超过140的天数,求X的分布列和数学期望;
(3)根据这20天统计数据,预测今后该地区甲流疫情的发展趋势.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明用数列{an}记录某地区2019年12月份31天中每天是否下过雨,方法为:当第k天下过雨时,记ak=1,当第k天没下过雨时,记ak=﹣1(1≤k≤31);他用数列{bn}记录该地区该月每天气象台预报是否有雨,方法为:当预报第k天有雨时,记bk=1,当预报第k天没有雨时,记bk=﹣1(1≤k≤31);记录完毕后,小明计算出a1b1+a2b2+…+a31b31=25,那么该月气象台预报准确的的总天数为_____;若a1b1+a2b2+…+akbk=m,则气象台预报准确的天数为_____(用m,k表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】某市场调查发现,某种产品在投放市场的30天中,其销售价格![]() (元)和时间
(元)和时间![]() (天)(
(天)(![]() )的关系如图所示
)的关系如图所示
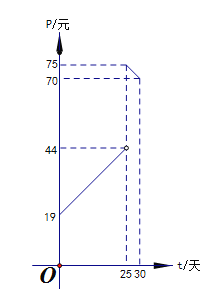
(1)写出销售价格![]() (元)和时间
(元)和时间![]() (天)的函数解析式;
(天)的函数解析式;
(2)若日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系是
(天)的函数关系是![]() (
(![]() ,
,![]() ),求该商品的日销售金额
),求该商品的日销售金额![]() (元)与时间
(元)与时间![]() (天)的函数解析式;
(天)的函数解析式;
(3)问该产品投放市场第几天时,日销售金额最高?最高值为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com