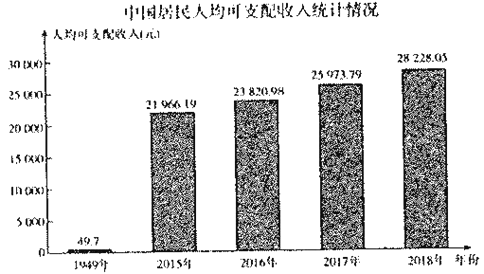
A.20l5年-2018年中国居民人均可支配收入与年份成正相关

B.2018年中居民人均可支配收入超过了1949年的500倍

C.2015年-2018年中国居民人均可支配收入平均超过了24000元

D.2015年-2018年中围居民人均可支配收入都超过了1949年的500倍

A.乙分8两，丙分8两，丁分8两B.乙分8两2钱，丙分8两，丁分7两8钱

C.乙分9两2钱，丙分8两，丁分6两8钱D.乙分9两，丙分8两，丁分7两

【题目】某快递公司收取快递费用的标准是：重量不超过的包裹收费元；重量超过的包裹，除收费元之外，超过的部分，每超出（不足，按计算）需再收元.该公司将最近承揽的件包裹的重量统计如下：

公司对近天，每天揽件数量统计如下表：

以上数据已做近似处理，并将频率视为概率.

（1）计算该公司未来天内恰有天揽件数在之间的概率；

（2）（i）估计该公司对每件包裹收取的快递费的平均值；

（ii）公司将快递费的三分之一作为前台工作人员的工资和公司利润，剩余的用作其他费用.目前前台有工作人员人，每人每天揽件不超过件，工资元.公司正在考虑是否将前台工作人员裁减人，试计算裁员前后公司每日利润的数学期望，并判断裁员是否对提高公司利润更有利？

在平面直角坐标系中，曲线的参数方程为（为参数）．

（1）求曲线的普通方程；

（2）经过点（平面直角坐标系中点）作直线交曲线于， 两点，若恰好为线段的三等分点，求直线的斜率．

【题目】已知函数.

（1）当时，求的极值；

（2）当函数有两个极值点，，总有成立，求整数t的最大值.

（1）完成列联表，并判断能否有99%的把握认为员工的饮食习惯与年龄有关？

（2）在45岁以上员工中按照饮食习惯进行分层抽样抽出一个容量为6的样本，从这6个人中随机抽取3个人，求这3个人都主食蔬菜的概率.

附：

.

【题目】设数列的前项和为，对于任意的，都有.

（1）求数列的首项及数列的递推关系式；

（2）若数列成等比数列，求常数的值，并求数列的通项公式；

（3）数列中是否存在三项、、，它们组成等差数列？若存在，请求出一组适合条件的项；若不存在，请说明理由.

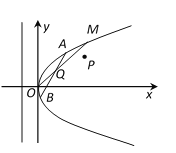
【题目】如图所示，在直角坐标系中，点到抛物线的准线的距离为，点是上的定点，、是上的两个动点，且线段的中点在线段上.

（1）抛物线的方程及的值；

（2）当点、分别在第一、四象限时，求的取值范围.

【题目】已知是定义在上的函数，满足.

（1）证明：2是函数的周期；

（2）当时，，求在时的解析式，并写出在（）时的解析式；

（3）对于（2）中的函数，若关于x的方程恰好有20个解，求实数a的取值范围.

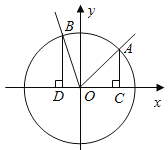
【题目】（本小题满分13分）如图，在直角坐标系中，角的顶点是原点，始边与轴正半轴重合．终边交单位圆于点，且，将角的终边按逆时针方向旋转，交单位圆于点，记．

（1）若，求；

（2）分别过作轴的垂线，垂足依次为，记的面积为，的面积为，若，求角的值．