
科目: 来源: 题型:
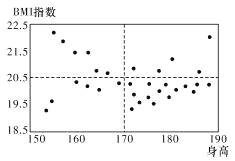
【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重;当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当BMI数值大于或等于20.5时,我们说体重较重;当![]() 数值小于20.5时,我们说体重较轻;身高大于或等于170
数值小于20.5时,我们说体重较轻;身高大于或等于170![]() 的我们说身高较高;身高小于170
的我们说身高较高;身高小于170![]() 的我们说身高较矮.
的我们说身高较矮.
(1)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图所示,请根据所得信息,完成下列列联表,并判断是否有95%的把握认为男体育特长生的身高对
指数的数据如散点图所示,请根据所得信息,完成下列列联表,并判断是否有95%的把握认为男体育特长生的身高对![]() 指数有影响;
指数有影响;
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(2)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献率
.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献率![]() (保留两位有效数字);
(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
残差 | 0.1 | 0.3 | 0.9 | -1.5 | -0.5 |
②通过残差分析,对于残差(绝对值)最大的那组数据,需要确认在样本点的采集中是否有人为的错误.已知通过重新采集发现,该组数据的体重应该为58(kg).请重新根据最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
(参考公式)
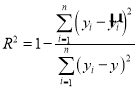 ,
,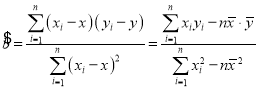 ,
,
![]() ,
,![]() ,
,
 (
(![]() ).
).
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(参考数据)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.当
两点.当![]() 时,
时,![]() 是椭圆
是椭圆![]() 的下顶点,且
的下顶点,且![]() 的周长为6.
的周长为6.

(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 、
、![]() 分别与直线
分别与直线![]() 交于
交于![]() 、
、![]() 点,证明:当
点,证明:当![]() 变化时,以线段
变化时,以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,且
,且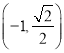 在椭圆E上.
在椭圆E上.
(1)求椭圆E的标准方程;
(2)已知垂直于x轴的直线![]() 交E于A、B两点,垂直于y轴的直线
交E于A、B两点,垂直于y轴的直线![]() 交E于C、D两点,
交E于C、D两点,![]() 与
与![]() 的交点为P,且
的交点为P,且![]() ,间:是否存在两定点M,N,使得
,间:是否存在两定点M,N,使得![]() 为定值?若存在,求出M,N的坐标,若不存在,请说明理由.
为定值?若存在,求出M,N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三棱柱![]() 的底面是正三角形,
的底面是正三角形,![]() 底面
底面![]() ,M为
,M为![]() 的中点.
的中点.
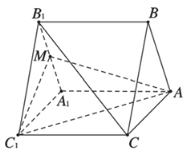
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,且沿侧棱
,且沿侧棱![]() 展开三棱柱的侧面,得到的侧面展开图的对角线长为
展开三棱柱的侧面,得到的侧面展开图的对角线长为![]() ,求作点
,求作点![]() 在平面
在平面![]() 内的射影H,请说明作法和理由,并求线段AH的长.
内的射影H,请说明作法和理由,并求线段AH的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy下,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C1在变换T:
为参数),曲线C1在变换T:![]() 的作用下变成曲线C2.
的作用下变成曲线C2.
(1)求曲线C2的普通方程;
(2)若m>1,求曲线C2与曲线C3:y=m|x|-m的公共点的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将
,AB的垂直平分线分别交AB,AC于D、E(图一),沿DE将![]() 折起,使得平面
折起,使得平面![]() 平面BDEC(图二).
平面BDEC(图二).

(1)若F是AB的中点,求证:![]() 平面ADE.
平面ADE.
(2)P是AC上任意一点,求证:平面![]() 平面PBE.
平面PBE.
(3)P是AC上一点,且![]() 平面PBE,求二面角
平面PBE,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲居住在城镇的![]() 处,准备开车到单位
处,准备开车到单位![]() 处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如:
处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如:![]() 算作两个路段:路段
算作两个路段:路段![]() 发生堵车事件的概率为
发生堵车事件的概率为![]() ,路段
,路段![]() 发生堵车事件的概率为
发生堵车事件的概率为![]() ).
).

(1)请你为甲选择一条由![]() 到
到![]() 的最短路线
的最短路线
(即此人只选择从西向东和从南向北的路线),
使得途中发生堵车事件的概率最小;
(2)设甲在路线![]() 中遇到的堵车次数为随机变量
中遇到的堵车次数为随机变量![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com