
科目: 来源: 题型:
【题目】某商场销售一种水果的经验表明,该水果每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为6元/千克时,每日可售出该水果52千克.
为常数.已知销售价格为6元/千克时,每日可售出该水果52千克.
(1)求![]() 的值;
的值;
(2)若该水果的成本为5元/千克,试确定销售价格![]() 的值,使商场每日销售该水果所获得的利润最大,并求出最大利润.
的值,使商场每日销售该水果所获得的利润最大,并求出最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(0,2),动点M到点A的距离比动点M到直线y=﹣1的距离大1,动点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)![]() x3+ax2+bx,且f′(﹣1)=0.
x3+ax2+bx,且f′(﹣1)=0.
(1)试用含a的代数式表示b;
(2)求f(x)的单调区间;
(3)令a=﹣1,设函数f(x)在x1、x2(x1<x2)处取得极值,记点M(x1,f(x1)),N(x2,f(x2)).证明:线段MN与曲线f(x)存在异于M,N的公共点.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在梯形ABCD中,AD∥BC,AB=BC![]() 2,E为AD的中点,O是AC与BE的交点,将△ABE沿BE翻折到图2中△A1BE的位置得到四棱锥A1﹣BCDE.
2,E为AD的中点,O是AC与BE的交点,将△ABE沿BE翻折到图2中△A1BE的位置得到四棱锥A1﹣BCDE.
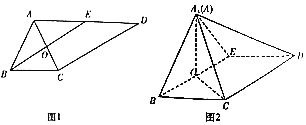
(1)求证:CD⊥A1C;
(2)若A1C![]() ,BE=2
,BE=2![]() ,求点C到平面A1ED的距离.
,求点C到平面A1ED的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4—5: 不等式选讲
已知函数f(x)=![]() 的定义域为R.
的定义域为R.
(Ⅰ)求实数m的取值范围;
(Ⅱ)若m的最大值为n,当正数a,b满足![]() =n时,求7a+4b的最小值.
=n时,求7a+4b的最小值.
查看答案和解析>>
科目: 来源: 题型:
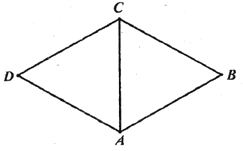
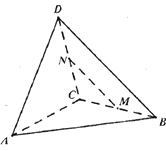
【题目】![]() 分别为菱形
分别为菱形![]() 的边
的边![]() 的中点,将菱形沿对角线
的中点,将菱形沿对角线![]() 折起,使点
折起,使点![]() 不在平面
不在平面![]() 内,则在翻折过程中,以下命题正确的是___________.(写出所有正确命题的序号)
内,则在翻折过程中,以下命题正确的是___________.(写出所有正确命题的序号)
①![]() 平面
平面![]() ;②异面直线
;②异面直线![]() 与
与![]() 所成的角为定值;③在二面角
所成的角为定值;③在二面角![]() 逐渐渐变小的过程中,三棱锥
逐渐渐变小的过程中,三棱锥![]() 的外接球半径先变小后变大;④若存在某个位程,使得直线
的外接球半径先变小后变大;④若存在某个位程,使得直线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.
(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com