
科目: 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,满足acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若△ABC的周长为3,求△ABC的内切圆面积S的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为弘扬民族古典文化,学校举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确给改选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() 的概率;
的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为
(t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若直线l与曲线C相交于A,B两点,求△AOB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,![]() ,过动点
,过动点![]() 作
作![]() ,垂足
,垂足![]() 在线段
在线段![]() 上且异于点
上且异于点![]() ,连接
,连接![]() ,沿
,沿![]() 将
将![]() 折起,使
折起,使![]() (如图2所示),
(如图2所示),
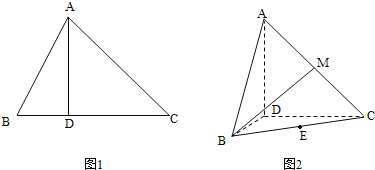
(1)当![]() 的长为多少时,三棱锥
的长为多少时,三棱锥![]() 的体积最大;
的体积最大;
(2)当三棱锥![]() 的体积最大时,设点
的体积最大时,设点![]() 分别为棱
分别为棱![]() 的中点,试在棱
的中点,试在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]() ,并求
,并求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年国际乒联总决赛在韩国仁川举行,比赛时间为12月13﹣12月16日,在男子单打项目,中国队准备选派4人参加.已知国家一线队共6名队员,二线队共4名队员.
(1)求恰好有3名国家一线队队员参加比赛的概率;
(2)设随机变量X表示参加比赛的国家二线队队员的人数,求X的分布列;
(3)男子单打决赛是林高远(中国)对阵张本智和(日本),比赛采用七局四胜制,已知在每局比赛中,林高远获胜的概率为![]() ,张本智和获胜的概率为
,张本智和获胜的概率为![]() ,前两局比赛双方各胜一局,且各局比赛的结果相互独立,求林高远获得男子单打冠军的概率.
,前两局比赛双方各胜一局,且各局比赛的结果相互独立,求林高远获得男子单打冠军的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x-a|-![]() x(a>0).
x(a>0).
(1)若a=3,解关于x的不等式f(x)<0;
(2)若对于任意的实数x,不等式f(x)-f(x+a)<a2+![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的上顶点为
的上顶点为![]() ,以
,以![]() 为圆心椭圆的长半轴为半径的圆与
为圆心椭圆的长半轴为半径的圆与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,试探究直线
,试探究直线![]() 是否过定点?若过定点,求出该定点的坐标,若不过定点,请说明理由.
是否过定点?若过定点,求出该定点的坐标,若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com