
科目: 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目: 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
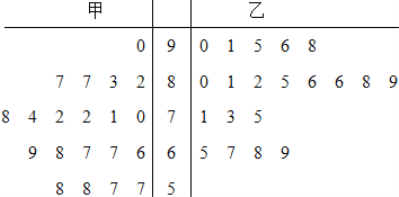
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 是R上的偶函数,对于
是R上的偶函数,对于![]() 都有
都有![]() 成立,且
成立,且![]() ,当
,当![]() ,且
,且![]() 时,都有
时,都有![]() .则给出下列命题:
.则给出下列命题:
①![]() ;
;
②函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ;
;
③函数![]() 在[﹣9,﹣6]上为减函数;④方程
在[﹣9,﹣6]上为减函数;④方程![]() 在[﹣9,9]上有4个根;
在[﹣9,9]上有4个根;
其中正确的命题序号是___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的离心率e
1(a>b>0)的离心率e![]() ,且点P(
,且点P(![]() ,1)在椭圆C上.
,1)在椭圆C上.
(1)求椭圆C的方程;
(2)若椭圆C的左焦点为F,右顶点为A,点M(s,t)(t>0)是椭圆C上的动点,直线AM与y轴交于点D,点E是y轴上一点,EF⊥DF,EA与椭圆C交于点G,若△AMG的面积为2![]() ,求直线AM的方程.
,求直线AM的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】2022年北京冬季奥运会即第24届冬季奥林匹克运动会,将在2022年2月4至2月20日在北京和张家口联合举行.某研究机构为了解大学生对冰壶运动的兴趣,随机从某大学学生中抽取了120人进行调查,经统计男生与女生的人数之比为11:13,男生中有30人表示对冰壶运动有兴趣,女生中有15人表示对冰壶运动没有兴趣.
(1)完成2×2列联表,并回答能否有99%的把握认为“对冰壶是否有兴趣与性别有关”?
有兴趣 | 没有兴趣 | 合计 | |
男 | 30 | ||
女 | 15 | ||
合计 | 120 |
(2)若将频率视为概率,现再从该校全体学生中,采用随机抽样的方法每次抽取1名学生,抽取5次,记被抽取的5名学生中对冰壶有兴趣的人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望和方差.
附:参考公式![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥K0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
K0 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】一个五位自然数![]() 数称为“跳跃数”,如果同时有
数称为“跳跃数”,如果同时有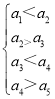 或
或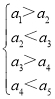 (例如13284,40329都是“跳跃数”,而12345,54371,94333都不是“跳跃数”),则由1,2,3,4,5组成没有重复数字且1,4不相邻的“跳跃数”共有_____个.
(例如13284,40329都是“跳跃数”,而12345,54371,94333都不是“跳跃数”),则由1,2,3,4,5组成没有重复数字且1,4不相邻的“跳跃数”共有_____个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com