
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,∠BCD=135°,PA⊥平面ABCD,AB=AC=PA=2,E,F,M分别为线段BC,AD,PD的中点.
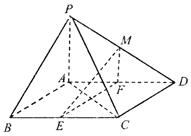
(1)求证:直线EF⊥平面PAC;
(2)求平面MEF与平面PBC所成二面角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() 的图象为C,下面结论正确的是( )
的图象为C,下面结论正确的是( )
A.函数f(x)的最小正周期是2π.
B.函数f(x)在区间![]() 上是递增的
上是递增的
C.图象C关于点![]() 对称
对称
D.图象C由函数g(x)=sin2x的图象向左平移![]() 个单位得到
个单位得到
查看答案和解析>>
科目: 来源: 题型:
【题目】唐代诗人李欣的是![]() 古从军行
古从军行![]() 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为
开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从
,若将军从![]() 出发,河岸线所在直线方程
出发,河岸线所在直线方程![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】2010-2018年之间,受益于基础设施建设对光纤产品的需求,以及个人计算机及智能手机的下一代规格升级,电动汽车及物联网等新机遇,连接器行业增长呈现加速状态.根据该折线图,下列结论正确的个数为( )

①每年市场规模量逐年增加;
②增长最快的一年为2013~2014;
③这8年的增长率约为40%;
④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模,数据方差更小,变化比较平稳
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,使得平面
同侧折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得到图2.
,得到图2.
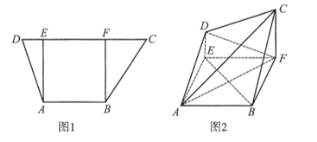
(1)证明:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,过A,B分别作CD的垂线,垂足分别为E,F,已知
,过A,B分别作CD的垂线,垂足分别为E,F,已知![]() ,
,![]() ,将梯形ABCD沿AE,BF同侧折起,使得平面
,将梯形ABCD沿AE,BF同侧折起,使得平面![]() 平面ABFE,平面
平面ABFE,平面![]() 平面BCF,得到图2.
平面BCF,得到图2.
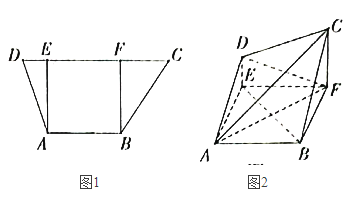
(1)证明:![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了200位高三学生的成绩进行统计分析得到如图所示频率分布直方图:
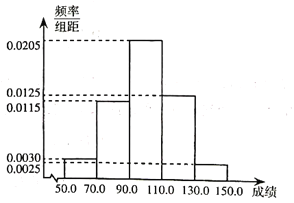
(1)计算这些学生成绩的平均值![]() 及样本方差
及样本方差![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)由频率分布直方图认为,这次成绩X近似服从正态分布![]() ,其中μ近似为样本平均数
,其中μ近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)求![]() ;
;
(ii)从高三学生中抽取10位学生进行面批,记![]() 表示这10位学生成绩在
表示这10位学生成绩在![]() 的人数,利用(i)的结果,求数学期望
的人数,利用(i)的结果,求数学期望![]() .
.
附:![]() ;
;
若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com