
【题目】如图1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,使得平面
同侧折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得到图2.
,得到图2.
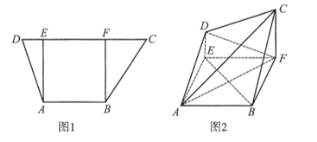
(1)证明:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+2φ)为偶函数,其中φ∈(0,![]() ),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
),则下列关于函数g(x)=sin(2x+φ)的描述正确的是( )
A.g(x)在区间[![]() ]上的最小值为﹣1
]上的最小值为﹣1
B.g(x)的图象可由函数f(x)的图象向上平移一个单位,再向右平移![]() 个单位长度得到
个单位长度得到
C.g(x)的图象的一个对称中心为(![]() ,0)
,0)
D.g(x)的一个单调递增区间为[0,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月15中秋节(农历八月十五)到来之际,某月饼销售企业进行了一项网上调查,得到如下数据:
男 | 女 | 合计 | |
喜欢吃月饼人数(单位:万人) | 50 | 40 | 90 |
不喜欢吃月饼人数(单位:万人) | 30 | 20 | 50 |
合计 | 80 | 60 | 140 |
为了进一步了解中秋节期间月饼的消费量,对参与调查的喜欢吃月饼的网友中秋节期间消费月饼的数量进行了抽样调查,得到如下数据:

已知该月饼厂所在销售范围内有30万人,并且该厂每年的销售份额约占市场总量的35%.
(1)试根据所给数据分析,能否有![]() 以上的把握认为,喜欢吃月饼与性别有关?
以上的把握认为,喜欢吃月饼与性别有关?
参考公式与临界值表: ,
,
其中:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(2)若忽略不喜欢月饼者的消费量,请根据上述数据估计:该月饼厂恰好生产多少吨月饼恰好能满足市场需求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:其中所有假命题的序号是_______.
①命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ;
;
②将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像;
的图像;
③幂函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() ;
;
④函数![]() 有两个零点.
有两个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图象为C,下面结论正确的是( )
的图象为C,下面结论正确的是( )
A.函数f(x)的最小正周期是2π.
B.函数f(x)在区间![]() 上是递增的
上是递增的
C.图象C关于点![]() 对称
对称
D.图象C由函数g(x)=sin2x的图象向左平移![]() 个单位得到
个单位得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和到直线
和到直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点作垂直于
,过点作垂直于![]() 轴的直线与曲线
轴的直线与曲线![]() 相交于两点,直线
相交于两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 相交于一点(交点位于线段
相交于一点(交点位于线段![]() 上,且与
上,且与![]() 不重合).
不重合).
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,四边形
相切时,四边形![]() 的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
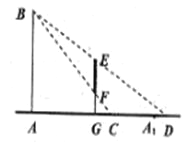
【题目】因客流量临时增大,某鞋店拟用一个高为50![]() (即
(即![]() )的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客
)的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客![]() 的眼睛
的眼睛![]() 到地面的距离为
到地面的距离为![]() (
(![]() )在区间
)在区间![]() 内,设支架
内,设支架![]() 高为
高为![]() (
(![]() )
)![]() ,
,![]() ,顾客可视的镜像范围为
,顾客可视的镜像范围为![]() (如图所示),记
(如图所示),记![]() 的长度为
的长度为![]() (
(![]() ).
).
(I)当![]() 时,试求
时,试求![]() 关于
关于![]() 的函数关系式和
的函数关系式和![]() 的最大值;
的最大值;
(II)当顾客的鞋![]() 在镜中的像
在镜中的像![]() 满足不等关系
满足不等关系![]() (不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求
(不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com