
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的焦点弦的弦长为
轴的焦点弦的弦长为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,
,![]() 互相垂直,直线
互相垂直,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于点
交于点![]() ,
,![]() 两点,直线
两点,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点.求
两点.求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为4.
,短轴长为4.
(1)求椭圆C的标准方程.
(2)设直线l过点(2,0)且与椭圆C相交于不同的两点A、B,直线![]() 与x轴交于点D,E是直线
与x轴交于点D,E是直线![]() 上异于D的任意一点,当
上异于D的任意一点,当![]() 时,直线BE是否恒过x轴上的定点?若过,求出定点坐标,若不过,请说明理由。
时,直线BE是否恒过x轴上的定点?若过,求出定点坐标,若不过,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,N为CD的中点,M是AC上一点.
中,N为CD的中点,M是AC上一点.
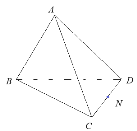
(1)若M为AC的中点,求证:AD//平面BMN;
(2)若![]() ,平面
,平面![]() 平面BCD,
平面BCD,![]() ,求直线AC与平面BMN所成的角的余弦值。
,求直线AC与平面BMN所成的角的余弦值。
查看答案和解析>>
科目: 来源: 题型:
【题目】某冰糖橙,甜橙的一种,云南著名特产,以味甜皮薄著称。该橙按照等级可分为四类:珍品、特级、优级和一级(每箱有5kg),某采购商打算订购一批橙子销往省外,并从采购的这批橙子中随机抽取100箱,利用橙子的等级分类标准得到的数据如下表:
等级 | 珍品 | 特级 | 优级 | 一级 |
箱数 | 40 | 30 | 10 | 20 |
(1)若将频率改为概率,从这100箱橙子中有放回地随机抽取4箱,求恰好抽到2箱是一级品的概率:
(2)利用样本估计总体,庄园老板提出两种购销方案供采购商参考:
方案一:不分等级卖出,价格为27元/kg;
方案二:分等级卖出,分等级的橙子价格如下:
等级 | 珍品 | 特级 | 优级 | 一级 |
售价(元/kg) | 36 | 30 | 24 | 18 |
从采购商的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这100箱橙子中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的是珍品等级,求x的分布列及数学期望E(X).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() ,(
,(![]() 为参数),将曲线
为参数),将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,纵坐标缩短为原来的
,纵坐标缩短为原来的![]() 后得到曲线
后得到曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 。
。
(1)求曲线![]() 的极坐标方程和直线l的直角坐标方程;
的极坐标方程和直线l的直角坐标方程;
(2)设直线l与曲线![]() 交于不同的两点A,B,点M为抛物线
交于不同的两点A,B,点M为抛物线![]() 的焦点,求
的焦点,求![]() 的值。
的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() (点
(点![]() 在
在![]() 轴上方),斜率为
轴上方),斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,且
,且![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)设椭圆![]() 的离心率为
的离心率为![]() ,当点
,当点![]() 为椭圆
为椭圆![]() 的右顶点时,
的右顶点时,![]() 的坐标为
的坐标为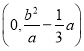 ,求
,求![]() 的值.
的值.
(2)若椭圆![]() 的方程为
的方程为![]() ,且
,且![]() ,是否存
,是否存![]() 在使得
在使得![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com