
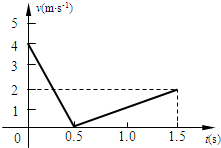 一物块以一定的初速度沿斜面向上滑,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系如图所示,g=10m/s2.求:
一物块以一定的初速度沿斜面向上滑,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系如图所示,g=10m/s2.求: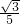 ,θ=30°
,θ=30°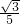 .
.

科目:高中物理 来源: 题型:
 (2011?梧州模拟)一物块以一定的初速度沿斜面向上滑出,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示,求:
(2011?梧州模拟)一物块以一定的初速度沿斜面向上滑出,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示,求:查看答案和解析>>
科目:高中物理 来源: 题型:
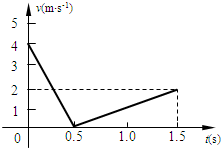 一物块以一定的初速度沿斜面向上滑,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系如图所示,g=10m/s2.求:
一物块以一定的初速度沿斜面向上滑,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系如图所示,g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 (A组) 一物块以一定的初速度沿斜面向上滑出,利用DIS实验系统,在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示.求:(g=10m/s2)
(A组) 一物块以一定的初速度沿斜面向上滑出,利用DIS实验系统,在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示.求:(g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:
 一物块以一定的初速度沿斜面向上滑出,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示,g=10m/s2.求:
一物块以一定的初速度沿斜面向上滑出,利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系图象如图所示,g=10m/s2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com