

���� �������������ṩ��������������ų��еİ뾶����������������˶��켣���뾶${R}_{2}^{\;}$��${R}_{1}^{\;}$�����������ݼ��ι�ϵ����нǺͱߣ����Ժ�˳��������������꣬��ʱ���ҳ�����Բ���Ե�Բ�Ľǣ�����$t=\frac{��}{360}T$��⣬���һ�ʶ��ܶ����������糡��û��������������A����һ�������ϣ������˶��ĺϳ���ֽ�˳�����
��� 
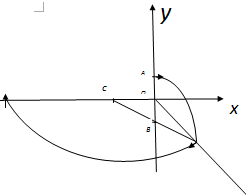 �⣺��1��������������ǿ�ų���������Բ���˶������������ṩ������$qvB=m\frac{{v}_{\;}^{2}}{R}$��$R=\frac{mv}{qB}$����${B}_{1}^{\;}$�ų��а뾶${R}_{1}^{\;}=\frac{mv}{qB}$��${B}_{2}^{\;}$�ų��а뾶${R}_{2}^{\;}=\frac{2mv}{qB}$�������������ӵ��˶��켣ͼ����ͼ
�⣺��1��������������ǿ�ų���������Բ���˶������������ṩ������$qvB=m\frac{{v}_{\;}^{2}}{R}$��$R=\frac{mv}{qB}$����${B}_{1}^{\;}$�ų��а뾶${R}_{1}^{\;}=\frac{mv}{qB}$��${B}_{2}^{\;}$�ų��а뾶${R}_{2}^{\;}=\frac{2mv}{qB}$�������������ӵ��˶��켣ͼ����ͼ
�ڴŸ�Ӧǿ��Ϊ${B}_{1}^{\;}$����ǿ�ų��У�Բ����B���뾶${R}_{1}^{\;}$���ڴŸ�Ӧǿ��Ϊ${B}_{2}^{\;}$����ǿ�ų��У�Բ��ΪC���뾶${R}_{2}^{\;}$
��������֪$\overline{OA}=\frac{mv}{2qB}$����$\overline{OB}=\frac{mv}{2qB}$��$\overline{OC}=\frac{\sqrt{3}}{2}\frac{mv}{qB}$
�ڶ��ξ���x��ʱ�Ľ��㵽ԭ��ľ���${R}_{2}^{\;}+\overline{OC}=\frac{2mv}{qB}+\frac{\sqrt{3}}{2}\frac{mv}{qB}=\frac{mv}{2qB}��4+\sqrt{3}��$
���Եڶ��ξ���x�������$��-\frac{mv}{2qB}��4+\sqrt{3}����0��$
��2���ɼ��ι�ϵ֪��OBC=60�㣬����$tan��=\frac{{R}_{1}^{\;}sin60��}{\overline{OB}+{R}_{1}^{\;}cos60��}=\frac{\sqrt{3}}{2}$
�ɼ��ι�ϵ֪����${B}_{1}^{\;}$�ų��е�Բ�Ľ�120�㣬��${B}_{2}^{\;}$�ų��е�Բ�Ľ�150��
${t}_{1}^{\;}=\frac{120��}{360��}{T}_{1}^{\;}=\frac{1}{3}\frac{2��m}{qB}=\frac{2��m}{3qB}$��${t}_{2}^{\;}=\frac{150��}{360��}{T}_{2}^{\;}=\frac{5}{12}\frac{2��m}{q\frac{B}{2}}=\frac{5��m}{3qB}$
���Եڶ��ξ���x����������ʱ��$t={t}_{1}^{\;}+{t}_{2}^{\;}=\frac{7��m}{3qB}$
��3�����ݶ��ܶ���֪�ӳ���㵽����A�㶯�ܲ��䣬�糡��û��������֪������A������Ϊһ�����棬�糡ǿ�ȷ���ֱ����б����
ˮƽ����${v}_{\;}^{2}=2\frac{q{E}_{x}^{\;}}{m}\frac{mv}{2qB}��4+\sqrt{3}��$���${E}_{x}^{\;}=��4+\sqrt{3}��vB$
��ֱ����${v}_{\;}^{2}=2\frac{q{E}_{y}^{\;}}{m}\frac{mv}{2qB}$���${E}_{y}^{\;}=vB$
�糡ǿ�ȵ���Сֵ$E=\sqrt{{E}_{x}^{2}+{E}_{y}^{2}}=\sqrt{��4+\sqrt{3}��_{\;}^{2}+1}vB$������ֱ������A����б����
�𣺣�1���ڶ��ξ���x��ʱ������$��-\frac{mv}{2qB}��4+\sqrt{3}����0��$��
��2��$tan��=\frac{\sqrt{3}}{2}$��A��������ڶ��ξ���x����������ʱ��$\frac{7��m}{3qB}$��
��3���ڵڶ�����ij�����ڣ���������㣩��һ��ǿ�糡��ʹ�����������ʱ��ͬ���ٶ��ֻص�A�㣮�����ӵ糡����Сֵ$\sqrt{��4+\sqrt{3}��_{\;}^{2}+1}vB$�ͷ���ֱ������A������б���£�
���� ����ǰ��С�ʱȽϻ���������С���ѶȽϴ���Ҫ������������ܴ���ĵ�����ƽ���˶�ȥ�������ջ�������˼��ܹؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ԭ�ӵĺ�ʽ�ṹ����ķ�����ֵ� | |
| B�� | �ڿ��ն�ЧӦ�У�����������뾧���еĵ�����ײʱ����һ���ֶ���ת�Ƹ����ӣ���˹���ɢ�����С | |
| C�� | һ�������䵽ij�ֽ����ϲ��ܷ������ЧӦ����������Ϊ������Ĺ�ǿ̫С | |
| D�� | �ü��ȡ���ѹ��ı��仯ѧ״̬�ķ��������ܸı�ԭ�Ӻ�˥��İ�˥�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
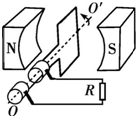 ��ͼ��ʾ��һС�ͷ��������N=100�Ѿ�����Ȧ����Ȧ���S=0.10m2����Ȧ�ܵ���r=1���������������¾�����Ȧ�ڴŸ�Ӧǿ��B=0.10T����ǿ�ų��У��Ժ㶨��ת��n=50r/s�ƴ�ֱ�ڴų�����Ĺ̶���OO'����ת�����������Ȧ������R=9���ĵ��蹹�ɱպϻ�·������Ȧƽ��ͨ��������ʱ��ʼ��ʱ����
��ͼ��ʾ��һС�ͷ��������N=100�Ѿ�����Ȧ����Ȧ���S=0.10m2����Ȧ�ܵ���r=1���������������¾�����Ȧ�ڴŸ�Ӧǿ��B=0.10T����ǿ�ų��У��Ժ㶨��ת��n=50r/s�ƴ�ֱ�ڴų�����Ĺ̶���OO'����ת�����������Ȧ������R=9���ĵ��蹹�ɱպϻ�·������Ȧƽ��ͨ��������ʱ��ʼ��ʱ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �ٶ��ڸı䣬����Ҳ�ڸı� | B�� | �ٶ��ڸı䣬���ܲ��� | ||
| C�� | �ٶȲ��䣬�����ڸı� | D�� | ���ܺ�����һ������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��̫��ϵ������A��̫�����뾶ΪR1��Բ���˶�������B���������˶���B�ڽ��յ㴦��̫�������ΪR2=2R1�����������ͬһƽ���ϣ��������˶�������ͼ�м�ͷ��ʾ����B�˶������յ�ʱ��Aǡ���˶���B��̫�������ϣ�A��B�漴����ij��ǿ�ҵ�����ö�Ѹ�ٺϲ���һ���µ����壬����������ʧ�ɺ��ԣ���֤����������̫�����˶����Ϊ��Բ��
��ͼ��̫��ϵ������A��̫�����뾶ΪR1��Բ���˶�������B���������˶���B�ڽ��յ㴦��̫�������ΪR2=2R1�����������ͬһƽ���ϣ��������˶�������ͼ�м�ͷ��ʾ����B�˶������յ�ʱ��Aǡ���˶���B��̫�������ϣ�A��B�漴����ij��ǿ�ҵ�����ö�Ѹ�ٺϲ���һ���µ����壬����������ʧ�ɺ��ԣ���֤����������̫�����˶����Ϊ��Բ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ֱ���ɻ����������������� | B�� | ���ػ������·ŵ����� | ||
| C�� | �������������ȼ������� | D�� | �����ع⻬б������»� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ˫�����ʵ���У�����˫���е�һ������ס����Ļ�ϳ���һ������ | |
| B�� | ��Ĥ�������Ʋ�����ԭ����ͬһ�����߾���Ĥǰ�������淴�������� | |
| C�� | �������ֽ�����˵���������д������ٶ���Դ�Ľ��ʽй��ܽ��� | |
| D�� | ����Ȼ��ͨ��ƫ��ƬP�����Թ�Ĵ�������Ϊ����תƫ��Ƭ����ǿ�Ȳ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
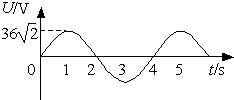
| A�� | 1sĩ�߿�ƽ�洹ֱ�ڴų���ͨ���߿�Ĵ�ͨ���仯��� | |
| B�� | 2sĩ�߿�ƽ�洹ֱ�ڴų���ͨ���߿�Ĵ�ͨ����� | |
| C�� | ������ѹ�����ֵΪ36$\sqrt{2}$V��Ƶ��Ϊ0.50Hz | |
| D�� | ������ѹ����ЧֵΪ36$\sqrt{2}$V������Ϊ4s |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com