
分析 这是一个双星的问题,两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,它们之间的万有引力提供各自的向心力,两颗恒星有相同的角速度和周期,结合牛顿第二定律和万有引力定律解决问题.
解答 解:两颗恒星的质量为${m}_{1}^{\;}$、${m}_{2}^{\;}$,做圆周运动的半径分别为${r}_{1}^{\;}$、${r}_{2}^{\;}$,角速度ω相等,周期相等
其中${r}_{1}^{\;}+{r}_{2}^{\;}=r$
根据万有引力定律和牛顿第二定律有:$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{r}_{\;}^{2}}={m}_{1}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{1}^{\;}={m}_{2}^{\;}\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{2}^{\;}$
解得:${m}_{2}^{\;}=\frac{4{π}_{\;}^{2}{r}_{1}^{\;}}{{GT}_{\;}^{2}}{r}_{\;}^{2}$
${m}_{1}^{\;}=\frac{4{π}_{\;}^{2}{r}_{2}^{\;}}{G{T}_{\;}^{2}}{r}_{\;}^{2}$
双星系统的总质量为:$m={m}_{1}^{\;}+{m}_{2}^{\;}=\frac{4{π}_{\;}^{2}({r}_{1}^{\;}+{r}_{2}^{\;}){r}_{\;}^{2}}{G{T}_{\;}^{2}}$=$\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$
故答案为:$\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$
点评 本题是双星问题,与卫星绕地球运动模型不同,两颗星都绕同一圆心做匀速圆周运动,关键抓住条件:相同的角速度和周期.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中物理 来源: 题型:实验题
 一定质量的理想气体,状态从A→B→C→D→A的变化过程可用如图所示的p-V图线描述,图中p1、p2、V1、V2和V3为已知量.
一定质量的理想气体,状态从A→B→C→D→A的变化过程可用如图所示的p-V图线描述,图中p1、p2、V1、V2和V3为已知量.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,质量为m的小球用一根细线和一根轻弹簧悬挂起来,小球静止时,细线水平,而弹簧与竖直成θ角.现将细线剪断,则下列判断正确的是( )
如图所示,质量为m的小球用一根细线和一根轻弹簧悬挂起来,小球静止时,细线水平,而弹簧与竖直成θ角.现将细线剪断,则下列判断正确的是( )| A. | 剪断细线前,细线中张力为$\frac{mg}{tanθ}$ | |
| B. | 剪断细线前,弹簧弹力大小为$\frac{mg}{cosθ}$ | |
| C. | 剪断细线瞬间,小球所受合力大小为mgsinθ | |
| D. | 剪断细线瞬间,小球所受合力大小为mgtanθ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
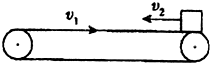 如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率vl匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率v2(v2>vl)滑上传送带,最终滑块又返回至传送带的右端,不考虑轴承摩擦,就上述过程,下列判断正确的有( )
如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率vl匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率v2(v2>vl)滑上传送带,最终滑块又返回至传送带的右端,不考虑轴承摩擦,就上述过程,下列判断正确的有( )| A. | 滑块返回传送带右端时的速率为v2 | |
| B. | 此过程中传送带对滑块做功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 | |
| C. | 此过程中电动机输出功为2mv12+mv1v2 | |
| D. | 此过程中滑块与传送带间因摩擦产生的热量为$\frac{1}{2}$m(v1+v2)2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
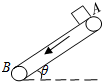 如图所示为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )
如图所示为粮袋的传送装置,已知AB间长度为L,传送带与水平方向的夹角为θ,工作时运行速度为v,粮袋与传送带间的动摩擦因数为μ,正常工作时工人在A点将粮袋放到运行中的传送带上,关于粮袋从A到B的运动,以下说法正确的是(设最大静摩擦力等于滑动摩擦力)( )| A. | 粮袋到达B点的速度与v比较,可能比v大,也可能与v相等或比v小 | |
| B. | 粮袋开始运动的加速度为g(sinθ-cosθ),若L足够大,则以后将一定以速度v做匀速运动 | |
| C. | 若μ≤tanθ,则粮袋从A到B一定一直是做加速运动 | |
| D. | 不论μ多大,粮袋从A到B一直匀加速运动,且a>gsinθ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 牛顿第一定律是牛顿第二定律的特例 | |
| B. | 在探索加速度与力、质量的关系时应用了控制变量的思想 | |
| C. | 物体的速度越大,物体的惯性越大 | |
| D. | 物体的合外力发生变化,加速度立即变化,速度也立即变化 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 需要对汽车提供足够的动力才能在公路上持续行驶,说明力是维持物体运动的原因 | |
| B. | 物体在粗糙的平面上减速滑行,初速度越大,滑行的时间越长,说明惯性的大小与速度有关 | |
| C. | 作用力和反作用力,都是同种性质的力,且同时产生,同时消失 | |
| D. | 作用力和反作用力等大反向合力为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
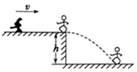 如图所示,高为h=0.8m的平台上,覆盖一层薄冰,现有一质量为50kg的滑雪爱好者,以一定的初速度向平台边缘滑去,着地前的速度方向与水平地面的夹角为45°.将滑雪者视为质点.g取10m/s2.求
如图所示,高为h=0.8m的平台上,覆盖一层薄冰,现有一质量为50kg的滑雪爱好者,以一定的初速度向平台边缘滑去,着地前的速度方向与水平地面的夹角为45°.将滑雪者视为质点.g取10m/s2.求查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com