
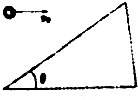
 小球以初速度v0正对着倾角为θ的斜面水平抛出,小球恰好垂直撞上斜面.
小球以初速度v0正对着倾角为θ的斜面水平抛出,小球恰好垂直撞上斜面.分析 (1)根据几何关系即可求出小球撞上斜面时与水平面的夹角.
(2)根据平行四边形定则求出小球撞在斜面上竖直分速度,结合平行四边形定则求出小球从O点运动到斜面的时间,根据运动的合成和分解可明确小球的合速度.
(3)根据水平位移和竖直位移,结合几何关系求出O点距斜面底端的高度和水平位移.
(4)根据运动的合成即可求出小球撞上斜面的位移大小和方向.
解答 解:(1)小球垂直撞在斜面上,有几何关系可知,速度与水平面的夹角为90°-θ,如图: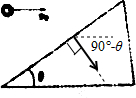
(2)小球垂直撞在斜面上,根据平行四边形定则知,
$\frac{{v}_{y}}{{v}_{0}}=tan(90°-θ)$,
解得vy=v0•tan(90°-θ)=$\frac{{v}_{0}}{tanθ}$
则小球的运动时间t=$\frac{{v}_{y}}{g}=\frac{{v}_{0}}{g•tanθ}$.
由几何关系,合速度:$v=\frac{{v}_{0}}{cos(90°-θ)}$=$\frac{{v}_{0}}{sinθ}$
(3)小球的水平位移x=${v}_{0}t=\frac{{{v}_{0}}^{2}}{gtanθ}$,
竖直位移y=$\frac{1}{2}g{t}^{2}=\frac{{{v}_{0}}^{2}}{2gta{n}^{2}θ}$
(4)小球撞上斜面的位移大小:
s=$\sqrt{{x}^{2}+{y}^{2}}$=$\frac{{v}_{0}^{2}}{2gtanθ}•\sqrt{4+\frac{1}{ta{n}^{2}θ}}$
位移与水平方向之间的夹角为α,则:
$tanα=\frac{y}{x}=\frac{\frac{{{v}_{0}}^{2}}{2gta{n}^{2}θ}}{\frac{{{v}_{0}}^{2}}{gtanθ}}=\frac{1}{2tanθ}$
答:(1)小球撞上斜面时速度与水平面的夹角是90°-θ;
(2)小球在空中运动的时间是$\frac{{v}_{0}}{g•tanθ}$;小球撞上斜面的速度大小是$\frac{{v}_{0}}{sinθ}$;
(3)小球撞上斜面时的下落竖直高度是$\frac{{{v}_{0}}^{2}}{2gta{n}^{2}θ}$,水平位移是$\frac{{{v}_{0}}^{2}}{gtanθ}$;
(4)小球撞上斜面的位移大小是$\frac{{v}_{0}^{2}}{2gtanθ}•\sqrt{4+\frac{1}{ta{n}^{2}θ}}$,位移方向与水平方向之间的夹角满足$tanα=\frac{1}{2tanθ}$.
点评 该题虽然要求解的问题比较多,但都是平抛运动的基本问题,解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,难度中等.


科目:高中物理 来源: 题型:选择题
| A. | 感应电动势E=$\frac{△Φ}{△t}$ | B. | 电容C=$\frac{Q}{U}$ | ||
| C. | 场强E=$\frac{F}{q}$ | D. | 磁感应强度B=$\frac{F}{IL}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
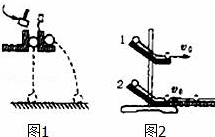
 如图所示,趣味运动会上运动员手持球拍托着乒乓球向前跑,球拍与水平方向的夹角为θ,运动员先以a=$\frac{10}{3}$m/s2匀加速向前跑,然后以速度v=8m/s匀速向前跑,不计球与拍之间的摩擦,球与拍始终保持相对静止,设跑动过程中空气对球的作用力水平且大小恒为f=0.1N,球的质量为m=0.01kg.重力加速度g取10m/s2,求:
如图所示,趣味运动会上运动员手持球拍托着乒乓球向前跑,球拍与水平方向的夹角为θ,运动员先以a=$\frac{10}{3}$m/s2匀加速向前跑,然后以速度v=8m/s匀速向前跑,不计球与拍之间的摩擦,球与拍始终保持相对静止,设跑动过程中空气对球的作用力水平且大小恒为f=0.1N,球的质量为m=0.01kg.重力加速度g取10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
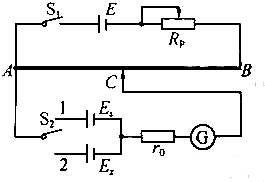 如图所示的电路可测电源的电动势,图中E为供电电源,Es为标准电源,Ex为待测电源,Rp是限流电阻,r0是电流表G的保护电阻.测量时,首先闭合开关S1,电阻丝AB上有一定的电势降落;接着将开关S2合到“1”位置,移动滑动触头C,使G指针指零,此时AC的长度为L1;再将S2合到“2”位置,移动滑动触头C,使G指针再指零,此时AC的长度为L2.
如图所示的电路可测电源的电动势,图中E为供电电源,Es为标准电源,Ex为待测电源,Rp是限流电阻,r0是电流表G的保护电阻.测量时,首先闭合开关S1,电阻丝AB上有一定的电势降落;接着将开关S2合到“1”位置,移动滑动触头C,使G指针指零,此时AC的长度为L1;再将S2合到“2”位置,移动滑动触头C,使G指针再指零,此时AC的长度为L2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 该星球的近地卫星速度大小是地球近地卫星速度大小的$\sqrt{\frac{Q}{P}}$倍 | |
| B. | 该星球的同步卫星速度大小是地球同步卫星速度大小的$\sqrt{\frac{Q}{P}}$倍 | |
| C. | 该星球质量是地球质量的$\frac{Q}{P}$倍 | |
| D. | 该星球密度是地球密度的$\frac{Q}{P}$倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
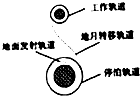 中国月球探测卫星“嫦娥号”简化后的路线示意图如图所示,卫星由地面发射后,先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动;然后从停泊轨道经过调控进入地月转移轨道;到达月球附近时,再次调控进入工作轨道做匀速圆周运动,这时卫星将开始对月球进行探测.已知地球与月球的质量之比为a,卫星的停泊轨道与工作轨道的轨道半径之比为b.则下列说法中正确的是( )
中国月球探测卫星“嫦娥号”简化后的路线示意图如图所示,卫星由地面发射后,先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动;然后从停泊轨道经过调控进入地月转移轨道;到达月球附近时,再次调控进入工作轨道做匀速圆周运动,这时卫星将开始对月球进行探测.已知地球与月球的质量之比为a,卫星的停泊轨道与工作轨道的轨道半径之比为b.则下列说法中正确的是( )| A. | 卫星从停泊轨道调控进入到地月转移轨道的过程中,卫星的机械能不守恒 | |
| B. | 卫星在停泊轨道运行的速度可能大于地球的第一宇宙速度 | |
| C. | 卫星在停泊轨道和工作轨道运行的线速度大小之比为$\sqrt{b}$:$\sqrt{a}$ | |
| D. | 卫星在停泊轨道和工作轨道运行的周期之比为b$\sqrt{b}$:$\sqrt{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com